
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量$\stackrel{∧}{y}$平均增加0.2个单位 | |
| D. | 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
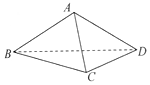 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )| A. |  | B. | 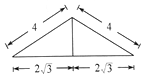 | C. | 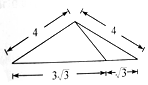 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不用必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
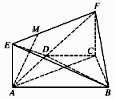 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com