
已知圆M过两点C(1,-1),D(-1,1),,且圆心M在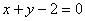 上.
上.
(1)求圆M的方程;
(2)设p是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
解:(1)设圆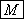 的方程为:(x-a)2+(y-b)2=r2(r>0).
的方程为:(x-a)2+(y-b)2=r2(r>0).
根据题意,得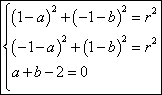 ﹍﹍﹍﹍﹍﹍﹍3分
﹍﹍﹍﹍﹍﹍﹍3分
解得a=b=1,r=2, ﹍﹍﹍﹍﹍﹍﹍5分
故所求圆M的方程为(x-1)2+(y-1)2=4. ﹍﹍﹍﹍﹍﹍﹍6分
(2)因为四边形PAMB的面积S=S△PAM+S△PBM=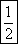 |AM|·|PA|+
|AM|·|PA|+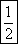 |BM|·|PB|,
|BM|·|PB|,
又|AM|=|BM|=2,|PA|=|PB|, 所以S=2|PA|, ﹍﹍﹍﹍﹍﹍﹍8分
而|PA|=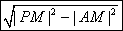 =
=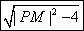 , 即S=2
, 即S=2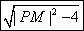 .
.
因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,
使得|PM|的值最小
所以|PM|min=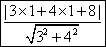 =3, ﹍﹍﹍﹍﹍﹍﹍10分
=3, ﹍﹍﹍﹍﹍﹍﹍10分
所以四边形PAMB面积的最小值为S=2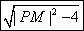 =2
=2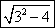 =2
=2 .
.


科目:高中数学 来源: 题型:
已知 是两条不同的直线,
是两条不同的直线,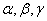 是三个不同的
是三个不同的
平面,下列命题中错误的是( )
A.若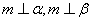 ,则
,则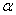 ∥
∥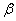
B.若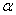 ∥
∥ ,
,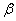 ∥
∥ ,则
,则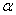 ∥
∥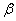
C.若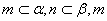 ∥
∥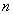 ,则
,则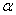 ∥
∥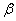
D.若 是异面直线,
是异面直线,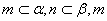 ∥
∥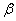 ,
,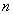 ∥
∥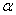 ,则
,则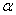 ∥
∥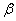
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com