练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若y＝f(x)的定义域是[0，2]，则函数f(x＋1)+f(2x－1)的定义域是

    [　　]
    A．

    [－1，1]

    B．

    C．

    D．

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2008年芜湖一中5月最后一模数学试卷(理科) 题型：022

    已知函数y＝f(x)

    ①函数y＝f(x)在闭区间上的最大值一定是极大值．

    ②若，则f(x)是以T＝6为周期的周期函数．

    ③若奇函数y＝f(x)在R上单调递增，那么必存在反函数y＝f－1(x)，且反函数也是奇函数，单调递增的．

    ④若y＝f(x)是定义在R上的可导函数，且＝0，则x0必定是f(x)的极值点．

    ⑤若f(x)是奇函数，则f(0)＝0一定成立．

    以上结论中错误的是________．

    查看答案和解析>>

    科目：高中数学 来源：吉林省长春市2010届高三第二次模拟数学理科试题 题型：022

    若y＝f(x)的图像如图所示，定义F(x)＝，则下列对F(x)的性质描述正确的有________

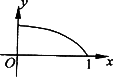
    (1)F(x)是[0，1]上的增函数；

    (2)(x)＝f(x)；

    (3)F(x)是[0，1]上的减函数；

    (4)x0∈[0，1]使得F(1)＝f(x0)

    查看答案和解析>>

    科目：高中数学 来源：浙江省09-10学年高一下学期期末提前招数学试题 题型：填空题

    若y＝f(x)是定义在(0，＋∞)上的单调减函数，且f(x)＜f(2x－2)，则x的取值范围______

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若y＝f(x)是定义在R上的函数，则y＝f(x)为奇函数的一个充要条件为


    1. A.
      存在某个x0∈R，使得f(x0)+f(-x0)＝0
    2. B.
      对任意x∈R，f(x)＝0都成立
    3. C.
      对任意的x∈R，都有f(x)+f(-x)＝0成立
    4. D.
      f(x)＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若y＝f(x)是定义在R上的奇函数，当x≥0时f(x)＝x2-2x，那么f(x)在R上的解析式是


    1. A.
      x(x-2)
    2. B.
      x(|x|-1)
    3. C.
      |x|(x-2)
    4. D.
      x(|x|-2)

    查看答案和解析>>

    同步练习册答案