Question

4．已知函数f（x）=x³-x及其图象曲线C
（1）当a=1时，求函数f（x）的单调区间及在（1，f（1））处的切线与曲线C的另一交点的横坐标
（2）证明：若对于任意非零实数x₁，曲线C与其点P₁（x₁，f（x₁））处的切线交于另一点P₂（x₂，f（x₂）），曲线C与其在点P₂（x₂，f（x₂））处的切线交于另一点P₃（x₃，f（x₃）），线段P₁P₂，P₂P₃与曲线C所围成封闭图形的面积分别记为S₁、S₂，则$\frac{S_1}{S_2}$为定值．

Answer 1

分析 （1）先求导数fˊ（x），在函数的定义域内解不等式fˊ（x）＞0解得的区间为增区间和fˊ（x）＜0解得的区间为减区间，曲线C在点（1，f（1））处的切线方程为y=2（x-1），即可得出在（1，f（1））处的切线与曲线C的另一交点的横坐标；
（2）先求出点P₁与点P₂的横坐标的关系，再求定积分求出围成封闭图形的面积S₁，利用同样的方法求出面积S₂即可．

解答 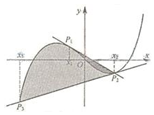（1）解：由f（x）=x³-x得f′（x）=3x²-1，
由f′（x）＞0，得f（x）的单调递增区间为（-∞，-$\frac{\sqrt{3}}{3}$），（$\frac{\sqrt{3}}{3}$，+∞）
由f′（x）＜0，得单调递减区间为（-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$）．
曲线C在点（1，f（1））处的切线方程为y=2（x-1），得x³-x=2x-2，x=-2或x=1（舍去）
故另一交点的横坐标为-2，…6
（ⅱ）曲线C与其在点P₁处的切线方程为$y=（3x_1^2-a）（x-{x_1}）+x_1^3-a{x_1}$，即$y=（3x_1^2-a）x-2x_1^3$
由$\left\{{\begin{array}{l}{y=（3x_1^2-a）x-2x_1^3}\\{y=x_1^3-a{x_1}}\end{array}}\right.$
得${x^3}-ax=（3x_1^2-a）x-2x_1^3$
解得x=x₁或x=-2x₁故x₂=-2x₁，进而有
S₁=|${∫}_{{x}_{1}}^{-2{x}_{1}}$（x³-3x₁³x+2x₁³）dx|=$\frac{27}{4}{{x}_{1}}^{4}$，用x₂代替x₁，重复上述计算过程，可得
x₃=-2x₂和S₂=$\frac{27}{4}{{x}_{2}}^{4}$，又x₂=-2x₁≠0，所以S₂≠0，
因此有$\frac{S_1}{S_2}$=$\frac{1}{16}$为定值．

点评 本小题主要考查函数、导数、定积分等基础知识，考查抽象概括能力、运算求解能力、推理论证能力，考查函数与方程思想、数形结合思想、化归与转化思想、特殊与一般思想．