
分析 (1)通过题意列出表达式20000+20000(1+10%)+20000(1+10%)2+20000(1+10%)3,进而计算可得结论;
(2)通过设从2008年开始n年后甲公司员工的年薪将超过乙公司员工的年薪,进而解不等式(8000+800+1000+200)×(1+25%)n>20000×(1+10%)n,计算即得结论.
解答 解:(1)20000+20000(1+10%)+20000(1+10%)2+20000(1+10%)3
=20000(1+1.1+1.12+1.13)
=20000×$\frac{1-1.{1}^{4}}{1-1.1}$
=92820(元);
(2)设从2008年开始n年后甲公司员工的年薪将超过乙公司员工的年薪,
则(8000+800+1000+200)×(1+25%)n>20000×(1+10%)n,
整理得:$(\frac{1.25}{1.1})^{n}$>2,
∴n>$lo{g}_{\frac{1.25}{1.1}}$2=$\frac{lg2}{lg\frac{1.25}{1.1}}$=$\frac{lg2}{lg1.25-lg1.1}$=$\frac{0.30107}{0.0969-0.0414}$≈5.4,
∴n≥6,即至少从2014年开始甲公司员工的年薪将超过乙公司员工的年薪.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{78}{71}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | (-∞,-1)∪(1,+∞) | C. | $({\frac{1}{2},+∞})$ | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}π$ | B. | $\frac{5}{4}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
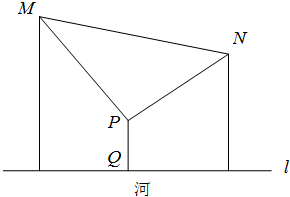 如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).
如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com