
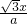 +
+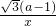 ,a≠0且a≠1.
,a≠0且a≠1. )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增,求a的值并写出函数的解析式;
,+∞)上单调递增,求a的值并写出函数的解析式;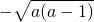 ,0),(0,
,0),(0,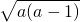 );
);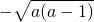 ),(
),(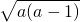 ,+∞).
,+∞).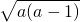 =
= ,且a>1,解得a=3,因此函数解析式为f(x)=
,且a>1,解得a=3,因此函数解析式为f(x)=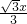 +
+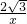 ( x≠0).
( x≠0).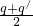 =
=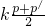 ,
,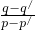 =
=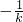 ,
, +
+ ,q′=
,q′=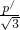 +
+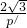 ,整理得k
,整理得k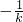 =
= ,解得k=
,解得k= 或k=
或k= .
. 及y=
及y=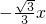 为曲线C的对称轴.
为曲线C的对称轴.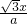 +
+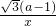 =
=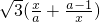 ,故需对a分①当a<0②当0<a<1③当a>1三种情况讨论函数的单调增区间
,故需对a分①当a<0②当0<a<1③当a>1三种情况讨论函数的单调增区间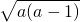 =
= ,且a>1,可求a的值,从而可得函数解析式
,且a>1,可求a的值,从而可得函数解析式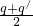 =
=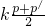 ,
,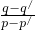 =
=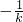 ,且q=
,且q= +
+ ,q′=
,q′=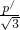 +
+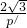 ,整理可求k
,整理可求k

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com