
[2012·山东卷] 如图1-6,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
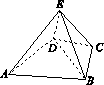
图1-6
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
证明:(1)取BD的中点O,连接CO,EO.
由于CB=CD,所以CO⊥BD,
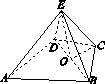
又EC⊥BD,EC∩CO=C,
CO,EC⊂平面EOC,
所以BD⊥平面EOC,
因此BD⊥EO,
又O为BD的中点,
所以BE=DE.
(2)证法一:取AB的中点N,连接DM,DN,MN,
因为M是AE的中点,
所以MN∥BE.
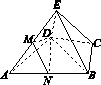
又MN⊄平面BEC,BE⊂平面BEC,
所以MN∥平面BEC,
又因为△ABD为正三角形,
所以∠BDN=30°,
又CB=CD,∠BCD=120°,
因此∠CBD=30°,
所以DN∥BC,
又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC,
又MN∩DN=N,
故平面DMN∥平面BEC,
又DM⊂平面DMN,
所以DM∥平面BEC.
证法二:
延长AD,BC交于点F,连接EF.
因为CB=CD,∠BCD=120°.
所以∠CBD=30°.
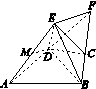
因为△ABD为正三角形.
所以∠BAD=60°,∠ABC=90°,
因此∠AFB=30°,
所以AB=![]() AF.
AF.
又AB=AD,
所以D为线段AF的中点.
连接DM,由点M是线段AE的中点,
因此DM∥EF.
又DM⊄平面BEC,EF⊂平面BEC,
所以DM∥平面BEC.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
[2012·山东卷] 如图1-3所示,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为________.
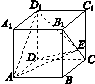
图1-3
查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·山东卷] 如图1-6,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.

图1-6
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考山东卷理科21)(本小题满分13分)
在平面直角坐标系![]() 中,
中,![]() 是抛物线
是抛物线![]()
![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上
上
位于第一象限内的任意一点,过![]() 三点的圆的圆心为
三点的圆的圆心为![]() ,点
,点![]() 到抛物线
到抛物线![]() 的准线
的准线
的距离为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)是否存在点![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() 若存在,求出点
若存在,求出点![]() 的坐标;
的坐标;
若不存在,说明理由;
(Ⅲ)若点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() ,
,![]() 与
与
圆![]() 有两个不同的交点
有两个不同的交点![]() ,求当
,求当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012·山东卷)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从![]() 中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )
中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )
A.232 B.252 C.472 D.484
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com