��չ̽����
��1����֪����Բ����x
2+y
2=1����x
2+��y-3��
2=1�����ɢ�ʽ��ȥ��ʽ�ɵ���Բ�ĶԳ��᷽�̣�������������������ΪԲ������¼����ƹ㣬��Ҫ��õ�һ����һ������⣬����֪����Ӧ��Ϊ���ƹ������һ���������ƹ������Ϊ
��֪����Բ���٣�x-a��2+��y-b��2=r2���ڣ�x-c��2+��y-d��2=r2�����ɢ�ʽ��ȥ��ʽ�ɵ���Բ�ĶԳ��᷽��
��֪����Բ���٣�x-a��2+��y-b��2=r2���ڣ�x-c��2+��y-d��2=r2�����ɢ�ʽ��ȥ��ʽ�ɵ���Բ�ĶԳ��᷽��
��
��2��ƽ�漸��������ȷ���⣺����������������һ�㵽���ߵľ���֮�͵��ڶ�ֵ����СΪ�߳���
����������д�������������弸�������Ƶ������⣺
��������������һ�㵽�ĸ���ľ���֮����һ����ֵ����СΪ�ⳤ��
��
��������������һ�㵽�ĸ���ľ���֮����һ����ֵ����СΪ�ⳤ��
��
��




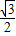 ����������д�������������弸�������Ƶ������⣺______
����������д�������������弸�������Ƶ������⣺______