
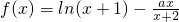 ,它在原点处的切线恰为x轴.
,它在原点处的切线恰为x轴.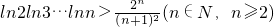 .
.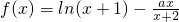 得,
得, -
-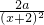 ,
,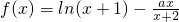 在原点处的切线恰为x轴.
在原点处的切线恰为x轴.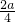 =0,
=0, ,
,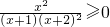 ,
, ,
, ,ln3>
,ln3>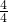 ,ln4>
,ln4> ,…,lnn>
,…,lnn>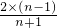 ,(n≥2),
,(n≥2),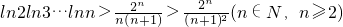 ,
,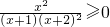 ,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论;
,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论; ,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.
,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
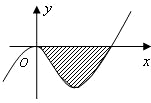 已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为| 27 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
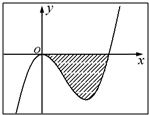 已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为| 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax |
| x+2 |
| ||
(n+1
|
查看答案和解析>>
科目:高中数学 来源:2015届江苏省江都市高一下学期期末考试数学试卷(解析版) 题型:填空题
已知函数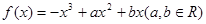 的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为
的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为 ,则a的值为
,则a的值为 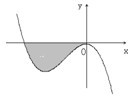
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com