
| π |
| 4 |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| π |
| 4 |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| 1 |
| 2 |
| 3 |
| 4 |


科目:高中数学 来源:2011-2012学年云南红河州高中毕业生统一检测理科数学试卷(解析版) 题型:选择题
给出以下四个命题:
(1)在 中, “
中, “ ”是“
”是“ ”的必要而非充分条件;
”的必要而非充分条件;
(2)函数 的最小正周期是
的最小正周期是 ;
;
(3)在 中,若
中,若

 ,则
,则 为钝角三角形;
为钝角三角形;
(4)在同一坐标系中,函数 与函数
与函数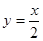 的图象有三个交点
的图象有三个交点
其中正确命题的个数是( )
A. 1  B.
2 C.
3
D. 4
B.
2 C.
3
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
①f(x)=![]() 在[0,1]上连续;
在[0,1]上连续;
②若f(x)是(a,b)内的连续函数,则f(x)在(a,b)内有最大值和最小值;
③![]()
![]() =4;
=4;
④若f(x)=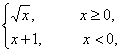 则
则![]() f(x)=0.
f(x)=0.
其中正确命题的序号是__________________.(请把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
给出以下四个命题:
①函数![]() 在R上是增函数的充分不必要条件是
在R上是增函数的充分不必要条件是![]() 对
对![]() R恒成立;
R恒成立;
②等比数列![]() ;
;
③把函数![]() 的图像向左平移1个单位,则得到的图象对应的函数解析式为
的图像向左平移1个单位,则得到的图象对应的函数解析式为![]() ;
;
④若数列{an}是等比数列,则a1+a2+a3+a4,a5+a6+a7+a8,a9+a10+a11+a12也一定成等比数列。
其中正确的是 ▲ .
查看答案和解析>>
科目:高中数学 来源: 题型:
给出以下四个命题:
①函数![]() 在R上是增函数的充分不必要条件是
在R上是增函数的充分不必要条件是![]() 对
对![]() R恒成立;
R恒成立;
②等比数列![]() ;
;
③把函数![]() 的图像向左平移1个单位,则得到的图象对应的函数解析式为
的图像向左平移1个单位,则得到的图象对应的函数解析式为![]() ;
;
④若数列{an}是等比数列,则a1+a2+a3+a4,a5+a6+a7+a8,a9+a10+a11+a12也一定成等比数列。
其中正确的是 ▲ .
查看答案和解析>>
科目:高中数学 来源: 题型:
以下四个命题中:
①![]() 在定义域上单调递增;
在定义域上单调递增;
②若锐角![]() 满足
满足![]() ,则
,则![]() ;
;
③函数![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() 则
则![]() ;
;
④要得到函数![]() 的图象,只需将
的图象,只需将![]() 的图象向左平移
的图象向左平移![]() 个单位;
个单位;
其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com