
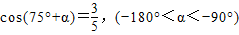 ,求sin(105°-α)+cos(375°-α)值;
,求sin(105°-α)+cos(375°-α)值;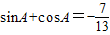 ,求sinA-cosA,tanA的值.
,求sinA-cosA,tanA的值.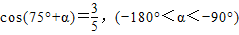 ,即可求出sin(105°-α)+cos(375°-α)的值;
,即可求出sin(105°-α)+cos(375°-α)的值;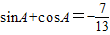 ,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.
,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.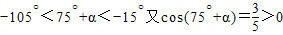
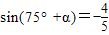

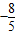
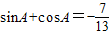 两边平方得
两边平方得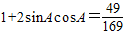
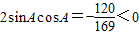
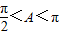
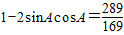

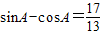
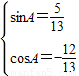
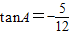


科目:高中数学 来源:2012-2013学年广东省珠海市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
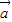 =(2,sinθ),
=(2,sinθ),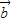 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.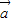 •
•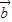 =
=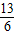 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;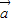 ∥
∥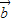 ,求sin(2θ+
,求sin(2θ+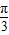 )的值.
)的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省日照市实验高中高一(下)期末数学复习试卷2(必修3、4)(解析版) 题型:解答题
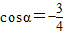 ,求sinα和tanα的值;(2)化简
,求sinα和tanα的值;(2)化简 •tanα
•tanα查看答案和解析>>
科目:高中数学 来源:2012年安徽省蚌埠二中高考数学一模试卷(文科)(解析版) 题型:解答题
 =(2,sinθ),
=(2,sinθ),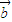 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.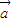 •
• =
=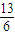 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;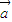 ∥
∥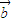 ,求sin(2θ+
,求sin(2θ+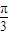 )的值.
)的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com