
【题目】已知圆![]() :
:![]() 内一点
内一点![]() ,
,![]() 点为圆
点为圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 连线交于点
连线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据线段中垂线的性质可得,|MP|=|MQ|,又|MQ|+|M![]() |=4,故有|M
|=4,故有|M![]() |+|MP|=4>|P
|+|MP|=4>|P![]() |,根据椭圆的定义判断轨迹椭圆,求出
|,根据椭圆的定义判断轨迹椭圆,求出![]() 值,即得椭圆的标准方程;
值,即得椭圆的标准方程;
(2)设![]() ,
,![]() ,设
,设![]() 的内切圆的半径为
的内切圆的半径为![]() ,当
,当![]() 最大,
最大,![]() 就最大,利用直线和椭圆的位置关系求出
就最大,利用直线和椭圆的位置关系求出![]() 最大值,进而可得
最大值,进而可得![]() 的最大值.
的最大值.
(1)由圆的方程可知,圆心![]() (1,0),半径等于4,设点M的坐标为
(1,0),半径等于4,设点M的坐标为![]() ,
,
∵PQ的垂直平分线交![]() Q于M,
Q于M,
∴|MP|=|MQ|.
又|MQ|+|M![]() |=4(半径),
|=4(半径),
∴|M![]() |+|MP|=4>|A
|+|MP|=4>|A![]() |=2.
|=2.
∴点M满足椭圆的定义,且2![]() =4,2
=4,2![]() =
=
∴![]() =2,
=2,![]() =1,
=1,![]() ,
,
∴点M的轨迹方程为![]() ;
;
(2)设![]() ,
,![]() ,设
,设![]() 的内切圆的半径为
的内切圆的半径为![]() ,因为
,因为![]() 的周长为
的周长为![]() ,
,![]() ,因此
,因此![]() 最大,
最大,![]() 就最大,
就最大,
![]() ,由题意知,直线
,由题意知,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,
,
由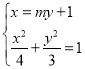 得
得![]() ,
,
所以![]() ,
,![]() ,
,
又因直线![]() 与椭圆
与椭圆![]() 交于不同的两点,故
交于不同的两点,故![]() ,即
,即![]() ,
,![]() ,则
,则![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
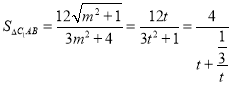 ,令
,令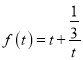 ,
,
由函数的性质可知,函数![]() 在
在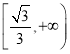 上是单调递增函数,即当
上是单调递增函数,即当![]() 时,
时,![]() 在
在![]() 上单调递增,因此有
上单调递增,因此有![]() ,所以
,所以![]() ,
,
即当![]() ,
,![]() 时,
时,![]() 最大,此时
最大,此时![]() ,故当直线
,故当直线![]() 的方程为
的方程为![]() 时,
时,![]() 内切圆半径的最大值为
内切圆半径的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知斜三棱柱![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,且
,且![]() .
.
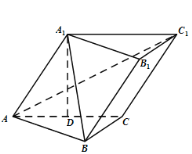
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的平面角为
的平面角为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
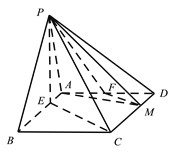
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,在亚洲热带地区广泛栽培.槟榔是重要的中药材,在南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
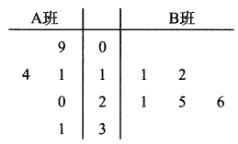
(1)你能否估计哪个班级学生平均每周咀嚼槟榔的颗数较多?
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率;
的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体A-BCD中,有两条棱的长为![]()
![]() ,其余棱的长度都为1;
,其余棱的长度都为1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范围,使得这样的四面体是存在的;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com