
【题目】已知函数![]() 的图象上存在点
的图象上存在点![]() ,函数
,函数![]() 的图象上存在点
的图象上存在点![]() ,且
,且![]() ,
,![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
若函数![]() 的图象上存在点
的图象上存在点![]() ,函数
,函数![]() 的图象上存在点
的图象上存在点![]() ,且
,且![]() ,
,![]() 关于
关于![]() 轴对称,则函数
轴对称,则函数![]() 的图象与函数y=x2+2的图象有交点,即方程
的图象与函数y=x2+2的图象有交点,即方程![]() =x2+2(x∈[
=x2+2(x∈[![]() ,e])有解.
,e])有解.
解:函数y=![]() 的图象与函数y=x2+2的图象关于x轴对称,
的图象与函数y=x2+2的图象关于x轴对称,
若函数![]() 的图象上存在点
的图象上存在点![]() ,函数
,函数![]() 的图象上存在点
的图象上存在点![]() ,且
,且![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,
则函数![]() 的图象与函数y=x2+2的图象有交点,
的图象与函数y=x2+2的图象有交点,
即方程![]() =x2+2(x∈[
=x2+2(x∈[![]() ,e])有解,
,e])有解,
即a=x2+2﹣8lnx(x∈[![]() ,e])有解,
,e])有解,
令f(x)=x2+2﹣![]() ,则f′(x)
,则f′(x)![]() ,
,
当x∈[![]() ,2)时,f′(x)<0,当x∈(2,e]时,f′(x)>0,
,2)时,f′(x)<0,当x∈(2,e]时,f′(x)>0,
故当x=2时,f(x)取最小值![]() ,
,
由f(![]() )
)![]() ,f(e)=
,f(e)=![]() ,
,
故当x=![]() 时,f(x)取最大值
时,f(x)取最大值![]() ,
,
故a∈![]() ,
,
故选:D.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】如图给出的是某高校土木工程系大四年级55名学生期末考试专业成绩的频率分布折线图(连接频率分布直方图中各小长方形上端的中点),其中组距为10,且本次考试中最低分为50分,最高分为100分.根据图中所提供的信息,则下列结论中正确的是( )
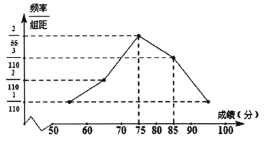
A. 成绩是75分的人数有20人
B. 成绩是100分的人数比成绩是50分的人数多
C. 成绩落在70-90分的人数有35人
D. 成绩落在75-85分的人数有35人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从10种不同的作物种子中选出6种分别放入6个不同的瓶子中,每瓶不空,如果甲、乙两种种子都不许放入第一号瓶子内,那么不同的放法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]()
![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点.
两点.
(1)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程;
轴相切,求该圆的方程;
(2)若直线![]() 与
与![]() 轴负半轴相交,求
轴负半轴相交,求![]() (
(![]() 为坐标原点)面积的最大值.
为坐标原点)面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 内一点
内一点![]() ,
,![]() 点为圆
点为圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 连线交于点
连线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 是双曲线在第一象限上的点,直线
是双曲线在第一象限上的点,直线![]() 交双曲线
交双曲线![]() 左支于点
左支于点![]() ,直线
,直线![]() 交双曲线
交双曲线![]() 右支于点
右支于点![]() ,若
,若![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的渐近线方程为( )
的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆柱![]() 的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,
的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,![]()
![]()
![]() :
:
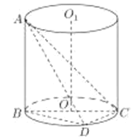
(1)求直线AC与平面ABD所成角的大小;
(2)求点B到平面ACD的距离;
(3)将四面体ABCD绕母线AB旋转一周,求由![]() 旋转而成的封闭几何体的体积;
旋转而成的封闭几何体的体积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com