练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从10种不同的作物种子中选出6种分别放入6个不同的瓶子中,每瓶不空,如果甲、乙两种种子都不许放入第一号瓶子内,那么不同的放法共有（　 ）

    A.种B.种C.种D.种

    【答案】D

    【解析】

    由排列组合中的分步原理分两步完成，先在除去甲、乙两种种子的8种不同的作物种子中选出1种放入第一号瓶子内, 然后在除去丙种子的剩余9种不同的作物种子中选出5种放入二号至六号瓶子内,运算即可得解.

    解：分两步完成，

    第一步：在除去甲、乙两种种子的8种不同的作物种子中选出1种放入第一号瓶子内,有种放法；不妨设取的为丙，

    第二步：在除去丙种子的剩余9种不同的作物种子中选出5种放入二号至六号瓶子内,有种放法；

    由排列组合中的分步原理可得：不同的放法共有种，

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个顶点是，离心率为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）已知矩形的四条边都与椭圆相切，设直线AB方程为，求矩形面积的最小值与最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线：.

    （Ⅰ）、是抛物线上不同于顶点的两点，若以为直径的圆经过抛物线的顶点，试证明直线必过定点，并求出该定点的坐标；

    （Ⅱ）在（Ⅰ）的条件下，抛物线在、处的切线相交于点，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数据，，，，的平均值为2，方差为1，则数据，，，相对于原数据（ ）

    A.一样稳定B.变得比较稳定C.变得比较不稳定D.稳定性不可以判断

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种类型的题目有，，，，5个选项，其中有3个正确选项，满分5分.赋分标准为“选对1个得2分，选对2个得4分,选对3个得5分，每选错1个扣3分，最低得分为0分”在某校的一次考试中出现了一道这种类型的题目，已知此题的正确答案为，假定考生作答的答案中的选项个数不超过3个.

    （1）若甲同学无法判断所有选项，他决定在这5个选项中任选3个作为答案，求甲同学获得0分的概率；

    （2）若乙同学只能判断选项是正确的，现在他有两种选择：一种是将AD作为答案，另一种是在这3个选项中任选一个与组成一个含有3个选项的答案，则乙同学的最佳选择是哪一种,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面是菱形，.

    （1）证明：平面平面；

    （2）若，，，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

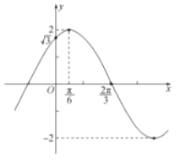
    【题目】已知函数的图象如图所示，令，则下列关于函数的说法中不正确的是（ ）

    A. 函数图象的对称轴方程为

    B. 函数的最大值为

    C. 函数的图象上存在点，使得在点处的切线与直线：平行

    D. 方程的两个不同的解分别为，，则最小值为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象上存在点，函数的图象上存在点，且，关于轴对称，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2﹣2x﹣4y+m＝0.

    （1）若圆C与直线l：x+2y﹣4＝0相交于M、N两点，且|MN|，求m的值；

    （2）在（1）成立的条件下，过点P（2，1）引圆的切线，求切线方程.

    查看答案和解析>>

    同步练习册答案