
【题目】已知抛物线![]() ,直线
,直线![]()
![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点.
两点.
(1)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程;
轴相切,求该圆的方程;
(2)若直线![]() 与
与![]() 轴负半轴相交,求
轴负半轴相交,求![]() (
(![]() 为坐标原点)面积的最大值.
为坐标原点)面积的最大值.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
试题(Ⅰ)联立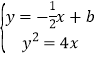 ,消
,消![]() 并化简整理得
并化简整理得![]() ,利用圆与
,利用圆与![]() 轴相切的位置关系得弦
轴相切的位置关系得弦![]() 从而确定
从而确定![]() 的值,进而求得该圆的方程;
的值,进而求得该圆的方程;
(Ⅱ)首先根据直线与抛物线的位置关系将弦![]() 的长度和原点到直线
的长度和原点到直线![]() 的距离均表示为
的距离均表示为![]() 的函数,并确定
的函数,并确定![]() 的取值范围,从而把
的取值范围,从而把![]() 的面积也表示为
的面积也表示为![]() 的函数,最后利用函数的最值求出
的函数,最后利用函数的最值求出![]() 的最大值.
的最大值.
试题解析:(Ⅰ)联立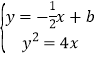 ,消
,消![]() 并化简整理得
并化简整理得![]() .
.
依题意应有![]() ,解得
,解得![]() .
.
设![]() ,则
,则![]() ,
,
设圆心![]() ,则应有
,则应有![]() .
.
因为以![]() 为直径的圆与
为直径的圆与![]() 轴相切,得到圆半径为
轴相切,得到圆半径为![]() ,
,
又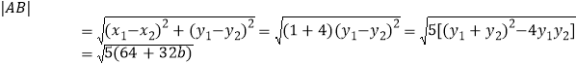 .
.
所以![]() ,
,
解得![]() .
.
所以![]() ,所以圆心为
,所以圆心为![]() .
.
故所求圆的方程为![]() .
.
(Ⅱ)因为直线![]() 与
与![]() 轴负半轴相交,所以
轴负半轴相交,所以![]() ,
,
又![]() 与抛物线交于两点,由(Ⅱ)知
与抛物线交于两点,由(Ⅱ)知![]() ,所以
,所以![]() ,
,
直线![]() :
:![]() 整理得
整理得![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() . 令
. 令![]() ,
,![]() ,
,
![]() ,
,
|
|
|
|
| + | 0 | - |
|
| 极大 |
|
由上表可得![]() 的最大值为
的最大值为![]() .所以当
.所以当![]() 时,
时,![]() 的面积取得最大值
的面积取得最大值![]() .
.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直接坐标系![]() 中,直线l的方程为x-y+4=0,曲线C的参数方程为
中,直线l的方程为x-y+4=0,曲线C的参数方程为![]() .
.
(I)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种类型的题目有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5个选项,其中有3个正确选项,满分5分.赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”在某校的一次考试中出现了一道这种类型的题目,已知此题的正确答案为
5个选项,其中有3个正确选项,满分5分.赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”在某校的一次考试中出现了一道这种类型的题目,已知此题的正确答案为![]() ,假定考生作答的答案中的选项个数不超过3个.
,假定考生作答的答案中的选项个数不超过3个.
(1)若甲同学无法判断所有选项,他决定在这5个选项中任选3个作为答案,求甲同学获得0分的概率;
(2)若乙同学只能判断选项![]() 是正确的,现在他有两种选择:一种是将AD作为答案,另一种是在
是正确的,现在他有两种选择:一种是将AD作为答案,另一种是在![]() 这3个选项中任选一个与
这3个选项中任选一个与![]() 组成一个含有3个选项的答案,则乙同学的最佳选择是哪一种,请说明理由.
组成一个含有3个选项的答案,则乙同学的最佳选择是哪一种,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示,令
的图象如图所示,令![]() ,则下列关于函数
,则下列关于函数![]() 的说法中不正确的是( )
的说法中不正确的是( )
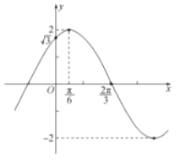
A. 函数![]() 图象的对称轴方程为
图象的对称轴方程为![]()
B. 函数![]() 的最大值为
的最大值为![]()
C. 函数![]() 的图象上存在点
的图象上存在点![]() ,使得在
,使得在![]() 点处的切线与直线
点处的切线与直线![]() :
:![]() 平行
平行
D. 方程![]() 的两个不同的解分别为
的两个不同的解分别为![]() ,
,![]() ,则
,则![]() 最小值为
最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的圆心在坐标原点O,且恰好与直线![]() 相切.
相切.
(Ⅰ)求圆C1的标准方程;
(Ⅱ)设点A为圆上一动点,AN垂直于x轴于点N,若动点Q满足![]()
(其中m为非零常数),试求动点Q的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当m=![]() 时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”其意思为:“今有白米一百八十石,甲、乙、丙三人来分,他们分得的白米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”请问:乙应该分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com