
 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.分析 (1)连接AC,证明AN⊥AD,利用平面与平面垂直的性质证明AN⊥平面ADEF,即可证明AN⊥DM;
(2)由(1)知,NA⊥平面ADEF,可得∠NMA为直线MN与平面ADEF所成的角,求出AN,AM,即可求直线MN与平面ADEF所成的角的正切值;
(3)利用三棱锥D-MAN的体积=三棱锥N-MAD的体积,即可求三棱锥D-MAN的体积.
解答 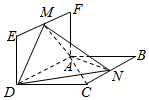 证明:(1)连接AC,在菱形ABCD中,
证明:(1)连接AC,在菱形ABCD中,
∵∠CBA=60°且AB=BC,∴△ABC为等边三角形.
∵N为BC的中点,∴AN⊥BC,
又∵BC∥AD,∴AN⊥AD,
∵平面ABCD⊥平面ADEF,AN?平面ADEF,平面ABCD∩平面ADEF=AD
∴AN⊥平面ADEF,
∵DM?平面ADEF,
∴AN⊥DM;
解:(2)由(1)知,NA⊥平面ADEF,
∴∠NMA为直线MN与平面ADEF所成的角,
∵四边形ADEF为矩形,AD=2AF=2,M是EF的中点,
∴AF=FM=1,
∴△AMF为等腰直角三角形,
∴AM=$\sqrt{2}$,
∵△ABC为边长为2的等边三角形且N是BC的中点,
∴AN=$\sqrt{3}$,
在Rt△NAM中,tan∠NMA=$\frac{AN}{AM}$=$\frac{\sqrt{6}}{2}$;
(3)∵四边形ADEF为矩形,M是EF的中点,AB=2AF=2,
∴ME=DE=1,且DM=AM=$\sqrt{2}$,
∴AD2=AM2+DM2,
∴∠AMD=90°,
∴S△AMD=$\frac{1}{2}•\sqrt{2}•\sqrt{2}$=1.
由(1)NA⊥平面ADEF,
∴三棱锥D-MAN的体积=三棱锥N-MAD的体积=$\frac{1}{3}•1•\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了直线与平面垂直的判定与性质,以及着重考查了棱锥的体积公式、线面角,考查空间想象能力、运算能力.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
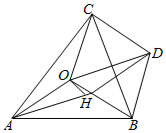 在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.
在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分
某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].
如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
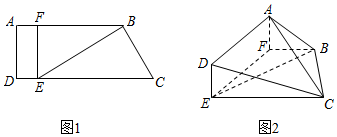 如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).
如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com