
设f(x)=ex-1.当a>ln 2-1且x>0时,证明:f(x)>x2-2ax.
证明:欲证f(x) >x2-2ax,即ex-1 >x2-2ax,
也就是ex-x2+2ax-1>0.
可令u(x)=ex-x2+2ax-1,则u′(x)=ex-2x+2a.
令h(x)=ex-2x+2a,则h′(x)=ex-2.
当x∈(-∞,ln 2)时,h′(x)<0,函数h(x)在(-∞,ln 2]上单调递减,当x∈(ln 2,+∞)时,h′(x)>0,函数h(x)在[ln 2,+∞)上单调递增.
所以h(x)的最小值为h(ln 2)=eln 2-2ln 2+2a
=2-2ln 2+2a.
因为a>ln 2-1,所以h(ln 2) >2-2ln 2+2(ln 2-1)=0,即h(ln 2)>0.
所以u′(x)=h(x)>0,即u(x)在R上为增函数.
故u(x)在(0,+∞)上为增函数.所以u(x)>u(0).
而u(0)=0,所以u(x)=ex-x2+2ax-1>0.
即当a>ln 2-1且x>0时,f(x)>x2-2ax.


科目:高中数学 来源: 题型:
如果命题p(n)对n=k(k∈N*)成立,则它对n=k+2也成立.若p(n)对n=2也成立,则下列结论正确的是( )
A.p(n)对所有正整数n都成立 B.p(n)对所有正偶数n都成立
C.p(n)对所有正奇数n都成立 D.p(n)对所有自然数n都成立
查看答案和解析>>
科目:高中数学 来源: 题型:
对于命题:若O是线段AB上一点,则有|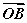 |·
|·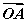 +|
+|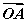 |·
|·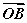 =0.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC·
=0.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC·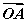 +S△OCA·
+S△OCA·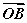 +S△OBA·
+S△OBA·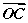 =
= ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A={x|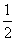 <2x<2},B={x|lgx>-1},则A∪B=( )
<2x<2},B={x|lgx>-1},则A∪B=( )
A.{x|x>-1} B.{x|-1<x<1}
C.{x|x>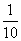 } D.{x|-1<x<10或x>10}
} D.{x|-1<x<10或x>10}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com