练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某电视台“挑战60秒”活动规定上台演唱:
    (I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).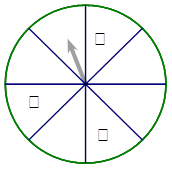

    （2）转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
    （3）演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
    ①求此人中一等奖的概率;
    ②设此人所得奖金为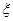,求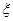的分布列及数学期望.

    (1)  (2)200

    解析试题分析：(1)由题意可知转一次奖获得一等奖的概率是，分成三类情况：①两次都中中一等奖②第一次中一等奖，第二次未中；③第一次未中一等奖，第二次中；
    (2)分别计算出奖金为每一种情况的概率，然后列出分布列，再计算出期望值即可.
    解: ①
    ②


    		0
    		100
    		200
    		300
    		400
    		500
    		600
    		700
    		1000










     
    故
    考点：相互独立事件的概率；离散型随机变量的分布列和数学期望

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答．
    （1）求张同学至少取到1道乙类题的概率；
    （2）已知所取的3道题中有2道甲类题，1道乙类题．设张同学答对每道甲类题的概率都是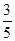，答对每道乙类题的概率都是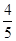，且各题答对与否相互独立．用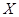表示张同学答对题的个数，求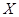的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某大学志愿者协会有6名男同学，4名女同学．在这10名同学中，3名同学来自数学学院，其余7名同学来自物理、化学等其他互不相同的七个学院．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）．
    （1）求选出的3名同学是来自互不相同学院的概率；
    （2）设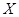为选出的3名同学中女同学的人数，求随机变量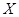的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为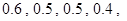各人是否需使用设备相互独立.
    （1）求同一工作日至少3人需使用设备的概率；
    （2）X表示同一工作日需使用设备的人数，求X的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （13分）（2011•重庆）某市公租房的房源位于A、B、C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，求该市的4位申请人中：
    （I）没有人申请A片区房源的概率；
    （II）每个片区的房源都有人申请的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：

    API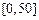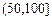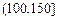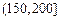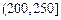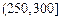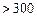
     
     
     
     
     
     
     
     
    空气质量
         		优
         		良
         		轻微污染
         		轻度污染
         		中度污染
         		中度重污染
         		重度污染
     
    天数
         		4
         		13
         		18
         		30
         		9
         		11
         		15
     
     
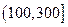    记某企业每天由空气污染造成的经济损失S（单位：元），空气质量指数API为ω。在区间[0，100]对企业没有造成经济损失；在区间对企业造成经济损失成直线模型（当API为150时造成的 经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的 经济损失为2000元；
    （1）试写出是S(ω)的表达式;
    （2）试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
    （3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？
    P(K2 ≥ k0)
         		0.25
         		0.15
         		0.10
         		0.05
         		0.025
         		0.010
         		0.005
         		0.001
     
    k0
         		1.323
         		2.072
         		2.706
         		3.841
         		5.024
         		6.635
         		7.879
         		10.828
     

     

     
    附：

     
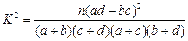
         		非重度污染
         		重度污染
         		合计
     
    供暖季
         		 
         		 
         		 
     
    非供暖季
         		 
         		 
         		 
     
    合计
         		 
         		 
         		100
     
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    高二年级的一个研究性学习小组在网上查知，某珍贵植物种子在一定条件下发芽成功的概率为，该研究性学习小组又分成两个小组进行验证性实验.
    （1）第1组做了5次这种植物种子的发芽实验（每次均种下一粒种子），求他们的实验至少有3次成功的概率；
    （2）第二小组做了若干次发芽试验（每次均种下一粒种子），如果在一次实验中种子发芽成功就停止实验，否则将继续进行下次实验，直到种子发芽成功为止，但发芽实验的次数最多不超过5次，求第二小组所做种子发芽实验的次数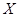的概率分布列和期望.      

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某学校一位教师要去某地参加全国数学优质课比赛，已知他乘火车、轮船、汽车、飞机直接去的概率分别为0.3、0.1、0.2、0.4.
    （1）求他乘火车或乘飞机去的概率；
    （2）他不乘轮船去的概率；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

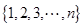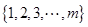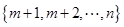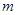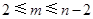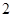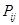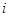    对有个元素的总体进行抽样，先将总体分成两个子总体 和(是给定的正整数，且)，再从每个子总体中各随机抽取个元素组成样本．用表示元素和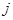同时出现在样本中的概率．
    (1)求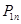的表达式(用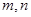表示)；
    (2)求所有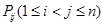的和．

    查看答案和解析>>

    同步练习册答案