
(13分)(2011•重庆)某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的4位申请人中:
(I)没有人申请A片区房源的概率;
(II)每个片区的房源都有人申请的概率.
(I)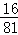 (II)
(II)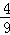
解析试题分析:(Ⅰ)解法一:首先分析所有的可能申请方式的情况数目,再分析没有人申请A片区房源的即所有的都申请BC区的申请方式的情况数目,由古典概型概率公式,计算可得答案;
解法二:视为独立重复试验中事件A恰好发生k次的情况,设对每位申请人的观察为一次试验,这是4次独立重复试验,记“申请A片区房源”为事件A,易得P(A),进而由独立重复试验中事件A恰好发生k次的概率计算公式计算可得答案;
(Ⅱ)根据题意,分析可得所有的可能申请方式的种数;而“每个片区的房源都有人申请”的申请方式的种数;
由古典概型概率公式,计算可得答案.
解:(I)由题意知本题是一个等可能事件的概率,
解法一:所有的可能申请方式有34种;而“没有人申请A片区房源的”的申请方式有24种;
记“没有人申请A片区房源”为事件A,
则P(A)=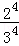 =
=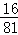 ;
;
解法二:设对每位申请人的观察为一次试验,这是4次独立重复试验,
记“申请A片区房源”为事件A,则P(A)= ;
;
由独立重复试验中事件A恰好发生k次的概率计算公式知:
“没有人申请A片区房源”的概率为P4(0)=C30•( )0(
)0(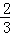 )4=
)4=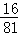 ;
;
(Ⅱ)所有的可能申请方式有34种;而“每个片区的房源都有人申请”的申请方式有C42•A33种;
记“每个片区的房源都有人申请”为事件B,
从而有P(B)=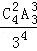 =
=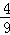 .
.
点评:本题考查等可能事件的概率,注意解题的格式应该规范,先有“记××为事件×”,进而又公式进行计算.


科目:高中数学 来源: 题型:解答题
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人. 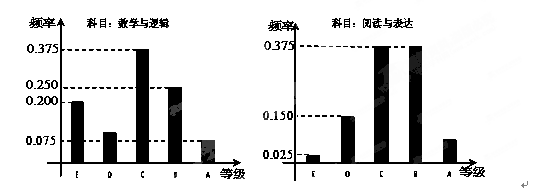
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分, 6人8分. 从这10中随机抽取两人,求两人成绩之和大于等于18的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取 次,每次抽取
次,每次抽取 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为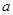 ,
,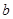 ,
,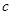 .
.
(Ⅰ)求“抽取的卡片上的数字满足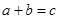 ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字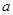 ,
,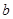 ,
,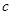 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将一颗质地均匀的正四面体骰子(四个面的点数分别为1,2,3,4)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)记事件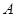 为“
为“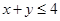 ”,求
”,求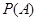 ;
;
(2)记事件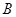 为“
为“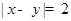 ”,求
”,求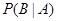 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为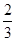 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品 研发成功,预计企业可获得
研发成功,预计企业可获得 万元,若新产品
万元,若新产品 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).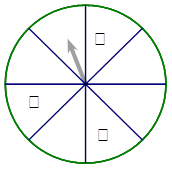
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为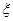 ,求
,求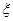 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“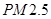 ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“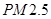 ” ” 小时平均浓度( 小时平均浓度(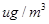 ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘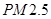 ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
做抛掷两颗骰子的试验:用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数,(1)写出试验的基本事件;(2)求事件“出现点数之和大于8”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数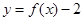 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com