
| kπ |
| 2 |
| π |
| 8 |
| 5π |
| 4 |
| π |
| 8 |
| 5π |
| 4 |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 8 |
| π |
| 8 |
| 5π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |


科目:高中数学 来源: 题型:
| 4π |
| 3 |
cos
| ||
sin
|
| 3 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| AB |
| AC |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建师大附中高一(下)期中数学试卷(解析版) 题型:填空题
 ;
; <0;
<0; ;
; 的角θ取值范围是(
的角θ取值范围是( +2kπ,
+2kπ,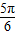 +2kπ),(k∈Z)
+2kπ),(k∈Z)查看答案和解析>>
科目:高中数学 来源: 题型:
已知下列四个命题:
(1)已知扇形的面积为![]() ,弧长为
,弧长为![]() ,则该扇形的圆心角为
,则该扇形的圆心角为![]() ;
;
(2)若![]() 是第二象限角,则
是第二象限角,则 ;
;
(3)在平面直角坐标系中,角![]() 的终边在直线
的终边在直线![]() 上,则
上,则![]() ;
;
(4) ![]() 的角
的角![]() 取值范围是
取值范围是![]()
其中正确命题的序号为 **** 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com