
分析 (1)由cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{m}{\sqrt{{m}^{2}+1}}=cos\frac{π}{4}$,求出m=1,由此能求出|$\overrightarrow{a}$-2$\overrightarrow{b}$|.
(2)由$\overrightarrow{a}+λ\overrightarrow{b}$=(1+λ,λ),($\overrightarrow{a}$+λ$\overrightarrow{b}$)与$\overrightarrow{b}$垂直,能求出实数λ的值.
解答 解:(1)∵$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(m,1),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$.
∴$\overrightarrow{a}•\overrightarrow{b}$=m,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{{m}^{2}+1}$,
cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{m}{\sqrt{{m}^{2}+1}}=cos\frac{π}{4}$,解得m=1,或m=-1(舍)
∴$\overrightarrow{a}-2\overrightarrow{b}$=(-1,-2),
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{(-1)^{2}+(-2)^{2}}$=$\sqrt{5}$.
(2)∵$\overrightarrow{a}+λ\overrightarrow{b}$=(1+λ,λ),
($\overrightarrow{a}$+λ$\overrightarrow{b}$)与$\overrightarrow{b}$垂直,
∴$(\overrightarrow a+λ\overrightarrow b)•\overrightarrow b=1+2λ=0$,
解得$λ=-\frac{1}{2}$.
点评 本题考查向量的模的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
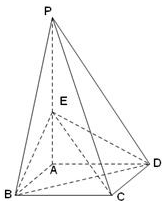 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
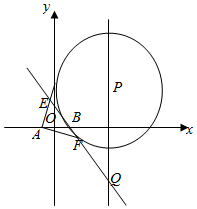 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1.75,2) | C. | (1.5,2) | D. | (1,1.5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com