
分析 (1)利用周期公式求函数的最小正周期,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(2)x间∈上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值.
解答 解:(1)∵$f(x)=\sqrt{2}cos(2x-\frac{π}{4})$,
∴函数f(x)的最小正周期为$T=\frac{2π}{2}=π$.
由$-π+2kπ≤2x-\frac{π}{4}≤2kπ$,
得$-\frac{3π}{8}+kπ≤x≤\frac{π}{8}+kπ$,
故函数f(x)的递调递增区间为$[-\frac{3π}{8}+kπ,\frac{π}{8}+kπ]$(k∈Z);
(2)∵$f(x)=\sqrt{2}cos(2x-\frac{π}{4})$在区间$[-\frac{π}{8},\frac{π}{8}]$上为增函数,
在区间$[\frac{π}{8},\frac{π}{2}]$上为减函数,
又$f(-\frac{π}{8})=0$,$f(\frac{π}{8})=\sqrt{2}$,$f(\frac{π}{2})=\sqrt{2}cos(π-\frac{π}{4})=-\sqrt{2}cos\frac{π}{4}=-1$,
故函数f(x)在区间$[-\frac{π}{8},\frac{π}{2}]$上的最大值为$\sqrt{2}$,此时$x=\frac{π}{8}$;最小值为-1,此时$x=\frac{π}{2}$.
点评 本题主要考查对三角函数的图象和性质的运用.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴上角的集合是{α|α=kπ,k∈Z} | |
| B. | 终边在y轴上角的集合是$\{α|α=\frac{π}{2}+kπ,k∈Z\}$ | |
| C. | 终边在坐标轴上角的集合是$\{α|α=k•\frac{π}{2},k∈Z\}$ | |
| D. | 终边在直线y=x上角的集合是$\{α|α=\frac{π}{4}+2kπ,k∈Z\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
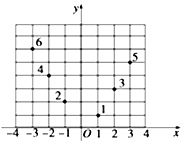 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )| A. | 1002 | B. | 1004 | C. | 1007 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com