
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2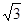 ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A.4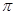 B.12
B.12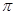 C.16
C.16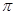 D.64
D.64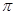
C
【解析】
试题分析:由三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA="2" 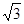 ,AB=1,AC=2,∠BAC=60°,知BC=
,AB=1,AC=2,∠BAC=60°,知BC=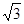 ,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=
,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=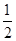 AC=1,由此能求出球O的半径,从而能求出球O的表面积。解:如图,
AC=1,由此能求出球O的半径,从而能求出球O的表面积。解:如图,

三棱锥S-ABC的所有顶点都在球O的球面上,∵SA⊥平面ABC,SA=2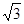 ,AB=1,AC=2,∠BAC=60°,∴BC=
,AB=1,AC=2,∠BAC=60°,∴BC=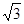 ,∴∠ABC=90°.∴△ABC截球O所得的圆O′的半径r=
,∴∠ABC=90°.∴△ABC截球O所得的圆O′的半径r=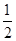 AC=1,∴球O的半径R=
AC=1,∴球O的半径R=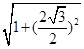 =2,∴球O的表面积S=4πR2=16π.故选C.
=2,∴球O的表面积S=4πR2=16π.故选C.
考点:球的表面积
点评:本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题时要关键.


科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:044
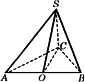
如图所示,已知三棱锥S-ABC中,SA=SB=SC,且AC2+BC2=AB2,由此可推出怎样的结论?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三棱锥S-ABC的各顶点都在一个半径为r的球面上,球心O在AB上,SO⊥底面ABC,AC=![]() r,则球的体积与三棱锥体积之比是( )
r,则球的体积与三棱锥体积之比是( )
A.π B.2π C.3π D.4π
查看答案和解析>>
科目:高中数学 来源:2013届浙江省嘉兴市八校高二上期中联考理科数学试卷(解析版) 题型:填空题
已知三棱锥S-ABC的侧棱和底面边长均为a,SO⊥底面ABC,垂足为O,
则SO= (用a表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com