
 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 的函数解析式
的函数解析式 ;
; 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
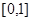 的函数
的函数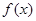 同时满足以下三个条件:
同时满足以下三个条件: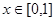 ,总有
,总有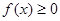 ;
;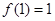 ;
; 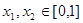 ,且
,且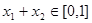 时,
时,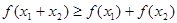 成立.
成立.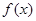 为“友谊函数”,求
为“友谊函数”,求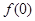 的值;
的值;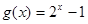 在区间
在区间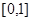 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;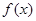 为“友谊函数”,假定存在
为“友谊函数”,假定存在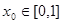 ,使得
,使得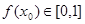 ,且
,且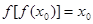 ,求证:
,求证: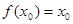 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =m?
=m? +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
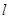 与曲线
与曲线 满足下列两个条件:
满足下列两个条件: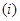 直线
直线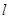 在点
在点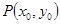 处与曲线
处与曲线 相切;
相切;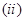 曲线
曲线 在
在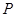 附近位于直线
附近位于直线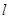 的两侧,则称直线
的两侧,则称直线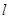 在点
在点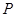 处“切过”曲线
处“切过”曲线 .
.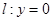 在点
在点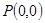 处“切过”曲线
处“切过”曲线 :
: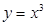
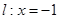 在点
在点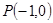 处“切过”曲线
处“切过”曲线 :
: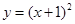
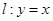 在点
在点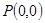 处“切过”曲线
处“切过”曲线 :
: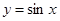
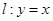 在点
在点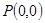 处“切过”曲线
处“切过”曲线 :
: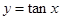
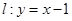 在点
在点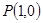 处“切过”曲线
处“切过”曲线 :
: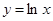
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.25元 | B.20.5元 | C.15元 | D.12.5元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com