
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
(2)讨论函数![]() 的单调性.
的单调性.
【答案】(1)![]() ;(2)见详解
;(2)见详解
【解析】
(1)利用等价转换的思想,紧接着分离参数,然后构造新的函数,通过观察新函数的单调性,根据新函数的值域与![]() 的关系,可得结果.
的关系,可得结果.
(2)利用导数研究含参数的函数的单调性,结合分类讨论,可得结果.
(1)依题意:
![]() ,
,
所以![]() 在
在![]() 上恒成立,
上恒成立,
故![]() ,而
,而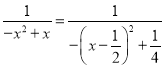 ,
,
当![]() 时,
时,![]() ,
,
故![]() ,解得
,解得![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.
(2)由(1)可得,
![]() ,
,
若![]() ,令
,令![]()
则![]() ;
;
若![]() 或
或![]() ,则
,则![]() ,
,
令![]() ,解得
,解得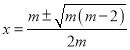 ,
,
记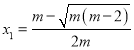 ,
, ,
,
其中![]() ;
;
①若![]() ,则
,则![]() ;
;
②若![]() ,
,
则![]() ,故当
,故当![]() 时,
时,![]() ;
;
③若![]() ,
,
则![]() ,其中
,其中![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
④若![]() ,
,
则![]() ,其中
,其中![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
综上所述:
当![]() 时,
时,
函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,
函数![]() 在
在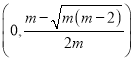 上单调递增,
上单调递增,
在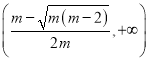 上单调递减;
上单调递减;
当![]() 时,
时,
函数![]() 在
在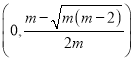 ,
,
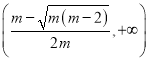 上单调递增,
上单调递增,
在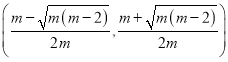 上单调递减.
上单调递减.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求证:
,求证: ![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入![]() ,
,![]() 的值分别为5,2,则输出
的值分别为5,2,则输出![]() 的值为( )
的值为( )
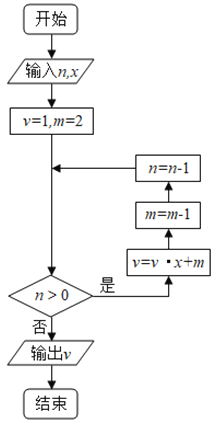
A.64B.68C.72D.133
查看答案和解析>>
科目:高中数学 来源: 题型:
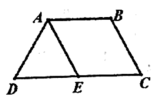
【题目】如图,等腰梯形![]() 中,
中,![]()
![]() ,
,![]() ,E为CD中点,将
,E为CD中点,将![]() 沿AE折到
沿AE折到![]() 的位置.
的位置.
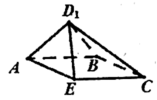
(1)证明:![]() ;
;
(2)当折叠过程中所得四棱锥![]() 体积取最大值时,求直线
体积取最大值时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为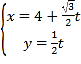 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com