练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）写出曲线的极坐标方程，并求出曲线与公共弦所在直线的极坐标方程；

    （2）若射线与曲线交于两点，与曲线交于点，且，求的值.

    【答案】（1）曲线的极坐标方程为，公共弦所在直线的极坐标方程（2）

    【解析】

    （1）先得到C1的一般方程，再由极坐标与直角坐标的互化公式得到极坐标方程，将，联立，得到公共弦所在直线的极坐标方程；

    （2）先求得|OA|，|OB|，可得|OA||OB|，化简可得到.

    （1）曲线的直角坐标方程为，将极坐标与直角坐标的互化公式：代入，

    可得曲线的极坐标方程为.

    联立与，得

    ∴曲线与公共弦所在直线的极坐标方程,（或和）

    （2）把，代入，，

    得；

    又，则=2，可得

    所以，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形，∥，，，平面平面，，.

    （1）求证：；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】自从新型冠状病毒爆发以来，全国范围内采取了积极的措施进行防控，并及时通报各项数据以便公众了解情况，做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.

    日期

    23

    24

    25

    26

    27

    28

    29

    30

    31

    时间

    1

    2

    3

    4

    5

    6

    7

    8

    9

    新增确诊人数

    15

    19

    26

    31

    43

    78

    56

    55

    57

    经过医学研究，发现新型冠状病毒极易传染，一个病毒的携带者在病情发作之前通常有长达14天的潜伏期，这个期间如果不采取防护措施，则感染者与一位健康者接触时间超过15秒，就有可能传染病毒.

    （1）将1月23日作为第1天，连续9天的时间作为变量x，每天新增确诊人数作为变量y，通过回归分析，得到模型用于对疫情进行分析.对上表的数据作初步处理，得到下面的一些统计量的值（部分数据已作近似处理）：，.根据相关数据，求该模型的回归方程（结果精确到0.1），并依据该模型预测第10天新增确诊人数.

    （2）如果一位新型冠状病毒的感染者传染给他人的概率为0.3，在一次12人的家庭聚餐中，只有一位感染者参加了聚餐，记余下的人员中被感染的人数为，求最有可能（即概率最大）的值是多少.

    附：对于一组数据，…，，其回归直线的斜率和截距的最小二乘估计分别为.

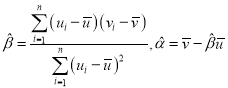    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，点，是圆上一动点，点在线段上，点在半径上，且满足.

    （1）当在圆上运动时，求点的轨迹的方程；

    （2）设过点的直线与轨迹交于点（不在轴上），垂直于的直线交于点，与轴交于点，若，求点横坐标的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，下述四个结论：

    ①是偶函数；

    ②的最小正周期为；

    ③的最小值为0；

    ④在上有3个零点

    其中所有正确结论的编号是（ ）

    A.①②B.①②③C.①③④D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为为参数），在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，点的极坐标为，直线的极坐标方程为．

    （1）求直线的直角坐标方程与曲线的普通方程；

    （2）若是曲线上的动点，为线段的中点，求点到直线的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球2次均未命中的概率为.

    （Ⅰ）求乙投球的命中率；

    （Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆的圆心的坐标为，且圆与直线：相切，过点的动直线与圆相交于，两点，直线与直线的交点为.

    （1）求圆的标准方程；

    （2）求的最小值；

    （3）问：是否是定值？若是，求出这个定值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在等腰梯形中，分别为的中点.现分别沿将和折起，使得平面平面，平面平面，连接，如图2．

    （1）求证：平面平面；

    （2）求多面体的体积．

    查看答案和解析>>

    同步练习册答案