
【题目】已知圆![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,且圆
,且圆![]() 与直线
与直线![]() :
:![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求![]() 的最小值;
的最小值;
(3)问:![]() 是否是定值?若是,求出这个定值;若不是,请说明理由.
是否是定值?若是,求出这个定值;若不是,请说明理由.
【答案】(1) ![]() . (2)
. (2) ![]() ; (3)
; (3) ![]() 是定值,定值为-10.
是定值,定值为-10.
【解析】
(1)根据圆![]() 与直线
与直线![]() :
:![]() 相切,即圆心到直线的距离等于半径,求出半径,即可写出圆
相切,即圆心到直线的距离等于半径,求出半径,即可写出圆![]() ;
;
(2)根据![]() 知当
知当![]() 为最大值
为最大值![]() 时,
时,![]() 有最小值;
有最小值;
(3)设![]() 中点为
中点为![]() ,
,![]() ,再设直线
,再设直线![]() ,联立方程组,计算即可得出
,联立方程组,计算即可得出![]() 。
。
解:(1)∵圆![]() 与直线
与直线![]() :
:![]() 相切,圆心为
相切,圆心为![]() ,
,
∴半径![]() ,
,
∴圆![]() 的方程为
的方程为![]() .
.
(2)∵![]() ,其中
,其中![]() 是圆心
是圆心![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() 最大时,
最大时,![]() 最小.
最小.
∵当![]() 是弦
是弦![]() 中点时,
中点时,![]() 最大,且
最大,且![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
(3)设![]() 中点为
中点为![]() ,则
,则![]() 即
即![]() ,∴
,∴![]() ,
,
且![]() ,
,
∴![]()
![]() .
.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 方程为
方程为![]() ,代入圆
,代入圆![]() 方程得
方程得![]() ,
,
∴![]() 中点
中点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点
的交点![]() 坐标为
坐标为![]() ,
,
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;
当![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 方程为
方程为![]() ,
,
由 ,得
,得![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() 是定值,定值为-10.
是定值,定值为-10.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定直线
到定直线![]() 的距离与到定点
的距离与到定点![]() 的距离之比为
的距离之比为![]() .
.
(1)求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,在
,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得曲线
,使得曲线![]() 上另有一点
上另有一点![]() ,满足
,满足![]() ,且
,且![]() ?若存在,求出所有符合条件的点
?若存在,求出所有符合条件的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”,其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,则该人第五天走的路程为( )
A. 6里B. 12里C. 24里D. 48里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
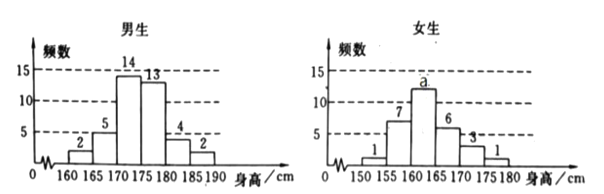
(1)估计该校男生的人数;并求出![]() 值
值
(2)估计该校学生身高在![]() 之间的概率;
之间的概率;
(3)从样本中身高在![]() 之间的女生中任选2人,求至少有1人身高在
之间的女生中任选2人,求至少有1人身高在![]() 之间的概率。
之间的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共有编号分别为1,2,3,4,5的五个座位,在甲同学不坐2号座位,乙同学不坐5号座位的条件下,甲、乙两位同学的座位号相加是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com