
如图,在平面直角坐标系xOy中,椭圆的中心在原点O,右焦点F在x轴上,椭圆与y轴交于A、B两点,其右准线l与x轴交于T点,直线BF交椭圆于C点,P为椭圆上弧AC上的一点.

(1)求证:A、C、T三点共线;
(2)如果 =3
=3 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.
(1)见解析(2)椭圆方程为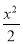 +y2=1.P点坐标为
+y2=1.P点坐标为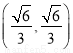
【解析】(1)证明:设椭圆方程为 =1(a>b>0)①,则A(0,b),B(0,-b),T
=1(a>b>0)①,则A(0,b),B(0,-b),T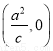 .
.
AT: =1②,BF:
=1②,BF: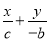 =1③,解得交点C
=1③,解得交点C ,代入①得
,代入①得
 =
=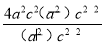 =1,满足①式,则C点在椭圆上,即A、C、T
=1,满足①式,则C点在椭圆上,即A、C、T
三点共线.
(2)【解析】
过C作CE⊥x轴,垂足为E,则△OBF∽△ECF.
∵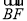 =3
=3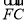 ,CE=
,CE=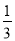 b,EF=
b,EF=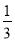 c,则C
c,则C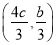 ,代入①得
,代入①得 =1,∴a2=2c2,b2=c2.设P(x0,y0),则x0+2
=1,∴a2=2c2,b2=c2.设P(x0,y0),则x0+2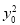 =2c2.此时C
=2c2.此时C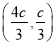 ,AC=
,AC=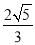 c,S△ABC=
c,S△ABC=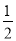 ·2c·
·2c·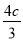 =
=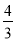 c2,
c2,
直线AC的方程为x+2y-2c=0,P到直线AC的距离为d=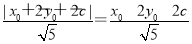 ,
,
S△APC=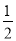 d·AC=
d·AC=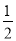 ·
·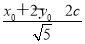 ·
·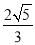 c=
c=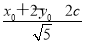 ·c.只须求x0+2y0的最大值,
·c.只须求x0+2y0的最大值,
(解法1)∵(x0+2y0)2=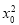 +4
+4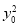 +2·2x0y0≤
+2·2x0y0≤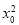 +4
+4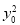 +2(
+2(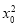 +
+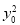 )=3(
)=3(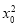 +2
+2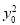 )=6c2,∴x0+2y0≤
)=6c2,∴x0+2y0≤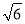 c.当且仅当x0=y0=
c.当且仅当x0=y0=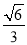 c时,(x0+2y0)max=
c时,(x0+2y0)max=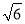 c.
c.
(解法2)令x0+2y0=t,代入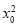 +2
+2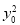 =2c2得(t-2y0)2+2
=2c2得(t-2y0)2+2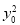 -2c2=0,即6
-2c2=0,即6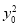 -4ty0+t2-2c2=0.Δ=(-4t)2-24(t2-2c2)≥0,得t≤
-4ty0+t2-2c2=0.Δ=(-4t)2-24(t2-2c2)≥0,得t≤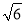 c.当t=
c.当t=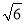 c,代入原方程解得x0=y0=
c,代入原方程解得x0=y0=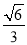 c.
c.
∴四边形的面积最大值为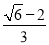 c2+
c2+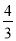 c2=
c2=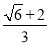 c2=
c2=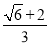 ,∴c2=1,a2=2,b2=1,此时椭圆方程为
,∴c2=1,a2=2,b2=1,此时椭圆方程为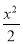 +y2=1.P点坐标为
+y2=1.P点坐标为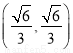 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第5课时练习卷(解析版) 题型:填空题
过直线x+y-2 =0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.
=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:解答题
直线l1:2x+y-4=0,求l1关于直线l:3x+4y-1=0对称的直线l2的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
设A1、A2与B分别是椭圆E: =1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
=1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
(1)求证: =1;
=1;
(2)P是椭圆E上异于A1、A2的一点,若直线PA1、PA2的斜率之积为- ,求椭圆E的方程;
,求椭圆E的方程;
(3)直线l与椭圆E交于M、N两点,且 ·
· =0,试判断直线l与圆C的位置关系,并说明理由.
=0,试判断直线l与圆C的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
如图,已知梯形ABCD中|AB|=2|CD|,点E满足 =λ
=λ ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当 ≤λ≤
≤λ≤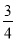 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:填空题
以双曲线-3x2+y2=12的焦点为顶点,顶点为焦点的椭圆的方程是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
给定椭圆C: =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F( ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点A是椭圆C的“准圆”与x轴正半轴的交点,B、D是椭圆C上的两相异点,且BD⊥x轴,求 ·
· 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点P,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,试判断l1,l2是否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:解答题
某工厂在试验阶段大量生产一种零件,这种零件有 、
、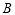 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为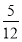 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件4个,设 表示其中合格品的个数,求
表示其中合格品的个数,求 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练文数学卷(解析版) 题型:选择题
 是
是 的( )条件
的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分又不必要
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com