A
分析:将已知等式记作①,左右两边平方,利用同角三角函数间的基本关系化简求出2sinαcosα的值,并根据2sinαcosα的值为负数及α的范围得到sinα大于0,cosα小于0,进而得到sinα-cosα大于0,然后利用完全平方公式及同角三角函数间的基本关系化简(sinα-cosα)
2,将2sinαcosα的值代入求出(sinα-cosα)
2的值,开方求出sinα-cosα的值,记作②,联立①②求出sinα与cosα的值,然后将所求的式子利用同角三角函数间的基本关系弦化切,即可求出tanα的值.
解答:将sinα+cosα=

①,左右两边平方得:(sinα+cosα)
2=sin
2α+cos
2α+2sinαcosα=

,
又sin
2α+cos
2α=1,∴1+2sinαcosα=

,即2sinαcosα=-

<0,
又α∈[0,π],∴sinα>0,cosα<0,即sinα-cosα>0,
∴(sinα-cosα)
2=sin
2α+cos
2α-2sinαcosα=1-2sinαcosα=

,
∴sinα-cosα=

②,或sinα-cosα=-

(舍去),
联立①②解得:sinα=

,cosα=-

,
则tanα=

=-

.
故选A
点评:此题考查了同角三角函数间的基本关系,以及完全平方公式的运用,熟练掌握基本关系是解本题的关键.

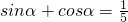 ,α∈[0,π],则tanα=
,α∈[0,π],则tanα=



 ①,左右两边平方得:(sinα+cosα)2=sin2α+cos2α+2sinαcosα=
①,左右两边平方得:(sinα+cosα)2=sin2α+cos2α+2sinαcosα= ,
, ,即2sinαcosα=-
,即2sinαcosα=- <0,
<0, ,
, ②,或sinα-cosα=-
②,或sinα-cosα=- (舍去),
(舍去), ,cosα=-
,cosα=- ,
, =-
=- .
.

 名校课堂系列答案
名校课堂系列答案