
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,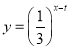 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某工厂今年前三个月生产某种产品的数量统计表如下:

为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟产品的月产量![]() 与月份
与月份![]() 的关系,模拟函数可选择二次函数
的关系,模拟函数可选择二次函数![]() (
(![]() 为常数且
为常数且![]() ),或函数
),或函数![]() (
(![]() 为常数).已知4月份的产量为1.37万件,请问用以上哪个函数作为模拟函数较好,请说明理由.
为常数).已知4月份的产量为1.37万件,请问用以上哪个函数作为模拟函数较好,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
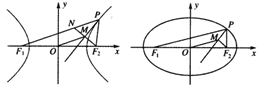
【题目】如图,P是双曲线![]() (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且![]() .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=![]() |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆![]() (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且![]() ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为
轴上,短轴长为![]() ,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点
,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点![]() 与
与![]() 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的方程.
(Ⅱ)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积.
的面积.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得经
,使得经![]() ,
, ![]() 为领边的平行四边形是菱形?若存在,求出
为领边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com