练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知正方形和矩形所在平面互相垂直， ， ．

    （1）求二面角的大小；

    （2）求点到平面的距离.

    【答案】（1）60°．（2）．

    【解析】试题分析：（1）先根据条件建立空间直角坐标系，设各点坐标，根据方程组求各面法向量，再根据向量数量积求夹角，最后根据二面角与向量夹角关系得结果（2）根据向量投影得点到平面的距离为再根据向量数量积求值

    试题解析： 正方形和矩形所在平面互相垂直，

    分别以AB，AD，AF为x，y，z轴建立空间直角坐标系，

    则A（0，0，0），B（，0，0）， C（， ，0）， D（0， ，0），

    E（, ，1），F（0，0，1）．

    （1）设平面CDE的法向量为平面BDE的法向量，

    由 解得.

    ∴ ，

    ∴ 二面角 B—DE—C等于60°．

    （2）

    ，

    ．设点到平面BDF的距离为h，则

    ∴．所以点F到平面BDE的距离为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设椭圆的方程为（），点为坐标原点，点， 的坐标分别为， ，点在线段上，满足，直线的斜率为．

    （1）求椭圆的方程；

    （2）若斜率为的直线交椭圆于， 两点，交轴于点（），问是否存在实数使得以为直径的圆恒过点？若存在，求的值，若不存在，说出理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C过点M（0，-2）、N（3，1），且圆心C在直线x+2y+1=0上．

    （1）求圆C的方程；

    （2）设直线ax-y+1=0与圆C交于A，B两点，是否存在实数a，使得过点P（2，0）的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据某水文观测点的历史统计数据，得到某河流水位（单位：米）的频率分布直方图如下：将河流水位在以上6段的频率作为相应段的概率，并假设每年河流水位互不影响.

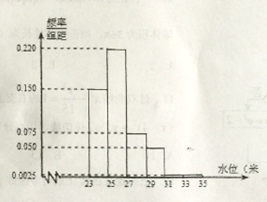
    （Ⅰ）求未来三年，至多有1年河流水位的概率（结果用分数表示）；

    （Ⅱ）该河流对沿河企业影响如下：当时，不会造成影响；当时，损失10000元；当时，损失60000元，为减少损失，现有三种应对方案：

    方案一：防御35米的最高水位，需要工程费用3800元；

    方案二：防御不超过31米的水位，需要工程费用2000元；

    方案三：不采用措施：试比较哪种方案较好，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f(x)＝ex－ax－1.

    （1）求f(x)的单调增区间；

    （2）若f(x)在定义域R内单调递增，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，，，点、分别为、的中点．

    （1）证明：平面；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，已知圆的圆心坐标为，半径为，以坐标原点为极点， 轴正半轴为极轴，建立极坐标系，直线的参数方程为： （为参数）

    (1)求圆和直线的极坐标方程；

    (2)点 的极坐标为，直线与圆相较于,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知射手甲射击一次，命中9环（含9环）以上的概率为0.56，命中8环的概率为0.22，命中7环的概率为0.12．

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （1）求甲射击一次，命中不足8环的概率；

    （2）求甲射击一次，至少命中7环的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    如图，在四棱锥P—ABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD=,底面ABCD为直角梯形，其中BC∥AD,AB⊥AD,AD=2AB=2BC=2，O为AD中点.

    (Ⅰ)求证:PO⊥平面ABCD；

    (Ⅱ)求异面直线PB与CD所成角的余弦值；

    (Ⅲ)求点A到平面PCD的距离.

    查看答案和解析>>

    同步练习册答案