
【题目】设椭圆![]() 的方程为
的方程为![]() (
(![]() ),点
),点![]() 为坐标原点,点
为坐标原点,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() (
(![]() ),问是否存在实数
),问是否存在实数![]() 使得以
使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说出理由.
的值,若不存在,说出理由.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】已知由自然数组成的![]() 元集合
元集合![]() ,非空集合
,非空集合![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() .
.
(1)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() ;
;
(2)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的元素总和;
的元素总和;
(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合![]() 的交替和是
的交替和是![]() ,集合
,集合![]() 的交替和为
的交替和为![]() .当
.当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的“交替和”的总和.
的“交替和”的总和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史,某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位: ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
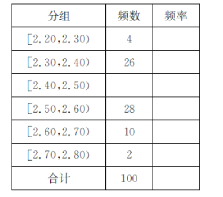
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是2.25作为代表.据此,估计这100个数据的平均值.
的中点值是2.25作为代表.据此,估计这100个数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对称轴为坐标轴的椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,则当
的斜率依次成等比数列,则当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 在区间
在区间![]() 上的值域
上的值域
(2)把函数![]() 图象所有点的上横坐标缩短为原来的
图象所有点的上横坐标缩短为原来的![]() 倍,再把所得的图象向左平移
倍,再把所得的图象向左平移![]() 个单位长度
个单位长度![]() ,再把所得的图象向下平移1个单位长度,得到函数
,再把所得的图象向下平移1个单位长度,得到函数![]() , 若函数
, 若函数![]() 关于点
关于点![]() 对称
对称
(i)求函数![]() 的解析式;
的解析式;
(ii)求函数![]() 单调递增区间及对称轴方程.
单调递增区间及对称轴方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com