
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性并求极值;
的单调性并求极值;
(Ⅱ)若点![]() 在函数
在函数![]() 上,当
上,当![]() ,且
,且![]() 时,证明:
时,证明: ![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2bcosC=acosC+ccosA.
(1)求角C的大小;
(2)若b=2,c=![]() ,求a及△ABC的面积.
,求a及△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的方程为
的方程为![]() (
(![]() ),点
),点![]() 为坐标原点,点
为坐标原点,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() (
(![]() ),问是否存在实数
),问是否存在实数![]() 使得以
使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说出理由.
的值,若不存在,说出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量, ![]() 获得本场比赛胜利,最终人机大战总比分定格
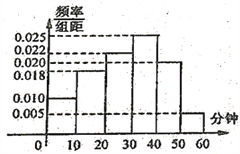
获得本场比赛胜利,最终人机大战总比分定格![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(Ⅰ)根据已知条件完成下面的列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名淡定生中的“围棋迷”人数为![]() 。若每次抽取的结果是相互独立的,求
。若每次抽取的结果是相互独立的,求![]() 的平均值和方差.
的平均值和方差.
附: 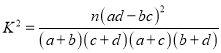 ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| td style="width:124.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年前三个月生产某种产品的数量统计表如下:

为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟产品的月产量![]() 与月份
与月份![]() 的关系,模拟函数可选择二次函数
的关系,模拟函数可选择二次函数![]() (
(![]() 为常数且
为常数且![]() ),或函数
),或函数![]() (
(![]() 为常数).已知4月份的产量为1.37万件,请问用以上哪个函数作为模拟函数较好,请说明理由.
为常数).已知4月份的产量为1.37万件,请问用以上哪个函数作为模拟函数较好,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com