
 ,给出下列四个命题:
,给出下列四个命题: (k∈Z)时,该函数取得最大值;
(k∈Z)时,该函数取得最大值; (k∈Z)时,f(x)<0.上述命题中正确的个数是______.
(k∈Z)时,f(x)<0.上述命题中正确的个数是______. +2kπ≤x≤
+2kπ≤x≤ +2kπ
+2kπ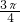 +2kπ<x<
+2kπ<x< +2kπ
+2kπ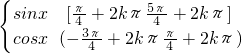 ,∴f(x)的值域为[-
,∴f(x)的值域为[- ,1]
,1] +2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.
+2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.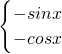 ≠f(x)
≠f(x) (k∈Z)
(k∈Z) ,1],f(x)取得最大值1时,得x=
,1],f(x)取得最大值1时,得x= +2kπ或x=2kπ(k∈Z),求解f(x)的最小正周期周期,利用定义f(x+T)=f(x)来判断,计算出π不是f(x)的最小正周期,经过验证第四个命题是对的.
+2kπ或x=2kπ(k∈Z),求解f(x)的最小正周期周期,利用定义f(x+T)=f(x)来判断,计算出π不是f(x)的最小正周期,经过验证第四个命题是对的.

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+90 |
| n |
| 181 |
| 13 |
| 181 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+90 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com