
已知函数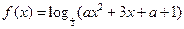
(1)当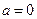 时,求函数
时,求函数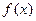 的定义域、值域及单调区间;
的定义域、值域及单调区间;
(2)对于 ,不等式
,不等式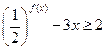 恒成立,求正实
恒成立,求正实 数
数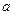 的取值范围.
的取值范围.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
心理学家发现,学生的接受能力依赖于老师引入概念 和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时
和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时 间为
间为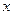 (单位:分),学生的接受能力为
(单位:分),学生的接受能力为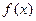 (
(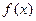 值越大,表示接受能力越强),
值越大,表示接受能力越强),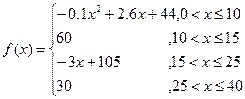
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;
(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某网民用电脑上因特网有两种方案可选:一是在家里上网,费用分为通讯费(即电话费)与网络维护费两部分。现有政策规定:通讯费为0.02元/分钟,但每月30元封顶(即超过30元则只需交30元),网络维护费1元/小时,但每月上网不超过10小时则要交10元;二是到附近网吧上网,价格为1.5元/小时。
(1)将该网民在某月内在家上网的费用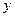 (元)表示为时间
(元)表示为时间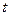 (小时)的函数;
(小时)的函数;
(2)试确定在何种情况下,该网民在家上网更便宜?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)函数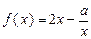 的定义域为
的定义域为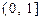 (
(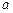 为实数).
为实数).
(1)当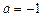 时,求函数
时,求函数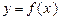 的值域;
的值域;
(2)若函数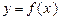 在定义域上是减函数,求
在定义域上是减函数,求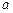 的取值范围;
的取值范围;
(3)函数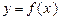 在
在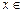
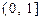 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时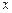 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com