练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    四棱台-ABCD，两底面是平行四边形，且=，过和B的平面将四棱台截去一个三棱锥，则剩余部分的体积是截去部分体积的

    [    ]

    A．14倍　　 B．13倍　　 C．7倍　　 D．6倍

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：阅读理解

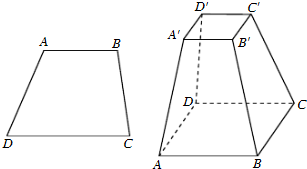    （必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
    设OE=x，∵△OAB∽△ODC，∴
    x
    x+h
    =
    a
    b
    ，即x=
    ah
    b-a
    ．
    ∴S梯形ABCD=S△ODC-S△OAB=
    1
    2
    b（x+h）-
    1
    2
    ax=
    1
    2
    （b-a）x+
    1
    2
    bh=
    1
    2
    （a+b）h．
    方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
    设梯形AMNB的高为x，MN=y，
    x
    h
    =
    y-a
    b-a
    ⇒y=a+
    b-a
    h
    x，∴S梯形ABCD=
    ∫
    h
    0
    （a+
    b-a
    h
    x）dx=（ax+
    b-a
    2h
    x2）
    |
    h
    0
    =ah+
    b-a
    2h
    •h2=
    1
    2
    （a+b）h．
    再解下面的问题：
    已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
    1
    3
    ×底面积×高）．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    如图，在正四棱柱ABCD－A1B1C1D1中，AA1＝AB，点E，M分别为A1B，C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N

    (Ⅰ)求证：EM∥平面A1B1C1D1；

    (Ⅱ)求二面角B－A1N－B1的正切值；

    (Ⅲ)(文)设A1A＝1，求棱台MNC1－BA1B1的体积V．

    (理)设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1，V2(V1＜V2)，求V1∶V2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题

    ①平行于同一直线的两个平面平行．

    ②平行于同一平面的两个平面平行．

    ③正方体ABCD－A1B1C1D1中，平面ACD1与平面A1BC1平行．

    ④四棱台ABCD－A1B1C1D1中，平面BCC1B1与平面ADD1A1相交．

    ⑤在两个平面内分别有一条直线，这两条直线不平行，那么这两个平面必相交．

    其中正确结论的序号是__________．

    查看答案和解析>>

    同步练习册答案