Question

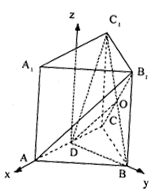
（08年西工大附中理）如图，已知正三棱柱ABC－ ，D是AC的中点，∠DC = 60°

    （Ⅰ）求证：A∥平面BD；

（Ⅱ）求二面角D－B－C的大小。

 

Answer 1

 

解析：解法一：

（Ⅰ）连结B₁C交BC于O，则O是BC的中点，连结DO。

∵在△AC中，O、D均为中点，

∴A∥DO   …………………………2分

∵A平面BD，DO平面BD，

∴A∥平面BD。…………………4分

（Ⅱ）设正三棱柱底面边长为2，则DC = 1。

    ∵∠DC = 60°，∴C= 。

作DE⊥BC于E。

∵平面BC⊥平面ABC，

∴DE⊥平面BC

作EF⊥B于F，连结DF，则 DF⊥B

∴∠DFE是二面角D-B-C的平面角……………………………………8分

在Rt△DEC中，DE=

在Rt△BFE中，EF = BE?sin

∴在Rt△DEF中，tan∠DFE =

∴二面角D－B－C的大小为arctan………………12分

解法二：以AC的中D为原点建立坐标系，如图，

设| AD | = 1∵∠DC =60°∴| C| = 。

     则A（1，0，0），B（0，，0），C（-1，0，0），

（1，0）， ，

（Ⅰ）连结C交B于O是C的中点，连结DO，则                  O.       =

∵A平面BD，

∴A∥平面BD.……………………………………………………………4分

（Ⅱ）=（-1，0，），

       设平面BD的法向量为n = （ x , y , z ），则

       即  则有= 0令z = 1

则n = （，0，1）…………………………………………………………8分

       设平面BC的法向量为m = ( x′ ,y′，z′)

   =（0，0，），，

  

 

   

      令y = -1，解得m = （，-1，0）

 

      二面角D ―B―C的余弦值为cos＜n , m＞＝

∴二面角D―B―C的大小为arc cos          …………１２分