
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.

(Ⅰ)证明 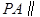 平面EDB;
平面EDB;
(Ⅱ)求EB与底面ABCD所成的角的正切值.
(Ⅰ)见解析;(Ⅱ)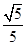 .
.
【解析】
试题分析:(Ⅰ)令AC、BD交于点O,连接OE,证明OE∥AP,即可证明AP∥面BDE;(Ⅱ)先找到直线与平面所成的角,令F是CD中点,又E是PC中点,连结EF,BF,可以证明EF⊥面ABCD,故∠EBF为面BE与面ABCD所成的角,在Rt⊿BEF中求出其正切值.
试题解析:(Ⅰ)令AC、BD交于点O,连接OE,∵O是AC中点,又E是PC中点
∴ OE∥AP 3分
又OE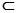 面BDE,AP
面BDE,AP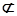 面BDE
5分
面BDE
5分
∴AP∥面BDE 6分
(Ⅱ)令F是CD中点,又E是PC中点,连结EF,BF
∴EF∥PD,又PD⊥面ABCD
∴EF⊥面ABCD 8分
∴∠EBF为面BE与面ABCD所成的角.
令PD=CD=2a
则CD=EF=a, BF=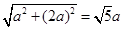 10分
10分
在Rt⊿BEF中,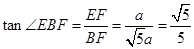
故BE与面ABCD所成角的正切是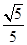 .
12分
.
12分
考点:线面平行的判定、直线与平面所成的角、勾股定理.


科目:高中数学 来源:2010-2011年广西省桂林中学高二下学期期中考试数学 题型:解答题
((本小题满分12分)
如图,在四棱锥 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
(1)证明 平面
平面 ;
;
(2)求异面直线 与
与 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2012届福建省三明市高三第一学期测试理科数学试卷 题型:解答题
如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 ,
, 是
是 的中点,
的中点, 是
是 的中点.
的中点.
(Ⅰ) 求证: ∥平面
∥平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求平面 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.

查看答案和解析>>
科目:高中数学 来源:2013届上海市高二年级期终考试数学 题型:解答题
(本题满分16分)
如图,在四棱锥 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
(1)证明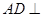 平面
平面 ;
;
(2)求异面直线 与
与 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源:2010年江苏省高二下学期期末考试附加卷数学卷 题型:解答题
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

(1)求PF:FB的值
(2)求平面 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2011届浙江省高三6月考前冲刺卷数学理 题型:解答题
(本小题满分14分)
如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面 ,
,

 在棱
在棱 上.
上.

(Ⅰ)当 时,求证
时,求证 平面
平面
(Ⅱ)当二面角 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com