
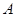 、
、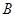 、
、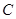 、
、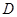 的坐标分别为
的坐标分别为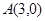 、
、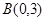 、
、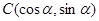 、
、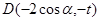 ,
,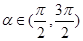
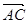 |=|
|=|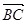 |,求角
|,求角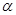 的值;
的值;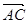 ·
·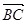 =
=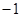 ,求
,求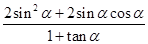 的值.
的值.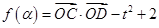 在定义域
在定义域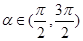 有最小值
有最小值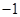 ,求
,求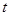 的值.
的值.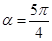 ;(2)
;(2)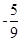 ;(3)
;(3)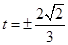 .
.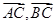 的坐标分别求得,即有
的坐标分别求得,即有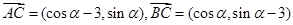 ,又根据
,又根据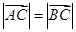 可以建立关于
可以建立关于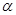 的方程,求得
的方程,求得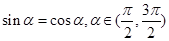 ,从而
,从而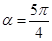 ;(2)由平面向量数量积的坐标表示,
;(2)由平面向量数量积的坐标表示,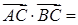
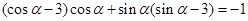 ,化简可得
,化简可得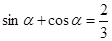 ,再将要求值的表达式化简为
,再将要求值的表达式化简为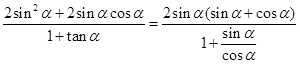
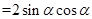 ,
,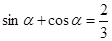 ,可求得
,可求得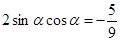 ,从而需求值的表达式的值为
,从而需求值的表达式的值为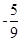 ;
;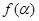
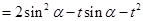 ,若令
,若令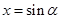 ,则问题等价于当
,则问题等价于当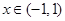 时,求使
时,求使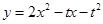 最小值为-1的
最小值为-1的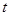 的值,显然
的值,显然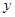 是关于
是关于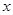 的开口向上的二次函数,若其在
的开口向上的二次函数,若其在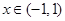 时,存在最小值,则必有对称轴
时,存在最小值,则必有对称轴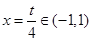 ,且当
,且当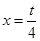 时,
时,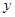 取到最小值-1,从而建立了关于
取到最小值-1,从而建立了关于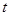 的方程,可解得
的方程,可解得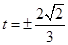 .
.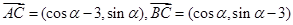 ,又∵
,又∵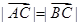 ,
,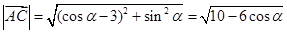 ,
,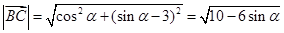
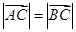 得
得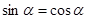 ,又
,又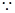
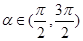 ,∴
,∴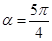 5分;
5分;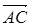 ·
·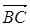 =
=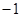 得
得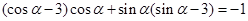 ,
,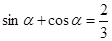 ① 6分
① 6分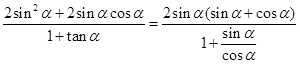
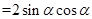 7分
7分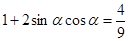 ∴
∴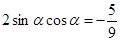 8分
8分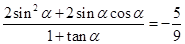 . 9分;
. 9分;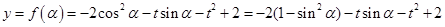
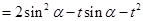 10分
10分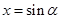 ,
, (
(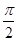 ,
,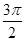 ),
),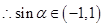 ,
,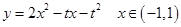 11分
11分 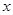 的二次函数开口向上,对称轴为
的二次函数开口向上,对称轴为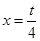 ,
,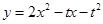 在
在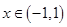 上存在最小值,则对称轴
上存在最小值,则对称轴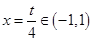
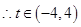 12分
12分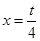 时,
时,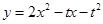 取最小值为
取最小值为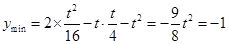
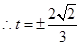 14分
14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com