
分析 由题意可得b=c,a-c=4$\sqrt{3}$-2$\sqrt{6}$,又a2-c2=b2,解方程可得a,b的值,进而得到椭圆方程.
解答 解:一个焦点与短轴的两端点的连线互相垂直,
即有焦点与短轴的两端点构成一个等腰直角三角形,
即有b=c,
又此焦点和长轴上较近的端点距离为4$\sqrt{3}$-2$\sqrt{6}$,
即为a-c=4$\sqrt{3}$-2$\sqrt{6}$,
又a2-c2=b2,
解得a=4$\sqrt{3}$,b=c=2$\sqrt{6}$,
则椭圆方程为$\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{24}$=1.
故答案为:$\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{24}$=1.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的求法,注意运用方程的思想方法,属于基础题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
 如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30$\sqrt{34}$ | B. | 60$\sqrt{34}$ | C. | 30$\sqrt{34}$+135 | D. | 135 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 14 | C. | 16 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
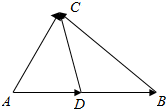 如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.
如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com