Question

16．在平面直角坐标系中，已知点A（-$\sqrt{3}$，0），B（$\sqrt{3}$，0），直线MA，MB相交于点M，它们的斜率之积为常数m（m≠0），且△MAB的面积最大值为$\sqrt{3}$，设动点M的轨迹为曲线E．
（Ⅰ）求曲线E的方程；
（Ⅱ）过曲线E外一点Q作E的两条切线l₁，l₂，若它们的斜率之积为-1，那么$\overrightarrow{QA}$$•\overrightarrow{QB}$是否为定值？若是，请求出该值；若不是，请说明理由．

Answer 1

分析 （Ⅰ）设M（x，y），由题意和斜率公式列出方程并化简，根据题意求出曲线E的方程；
（Ⅱ）设Q（x₀，y₀），由曲线E的方程和题意画出图象，由圆的切线的性质求出OQ，由两点之间的距离公式列出式子，由向量的坐标运算和数量积运算化简$\overrightarrow{QA}•\overrightarrow{QB}$，即可求出$\overrightarrow{QA}•\overrightarrow{QB}$为定值．

解答 解：（Ⅰ）设M（x，y），且A（-$\sqrt{3}$，0），B（$\sqrt{3}$，0），
由题意得k_MA•k_MB=m，即$\frac{y-0}{x+\sqrt{3}}•\frac{y-0}{x-\sqrt{3}}=m$（$x≠±\sqrt{3}$），
化简得，y²=m（x²-3）（m≠0），则mx²-y²=3m（$x≠±\sqrt{3}$），
∵△MAB的面积最大值为$\sqrt{3}$，∴$|y|≤\sqrt{3}$，
∴当m=-1时，方程为x²+y²=3满足条件，
则曲线E的方程是x²+y²=3（$x≠±\sqrt{3}$）；
（Ⅱ）$\overrightarrow{QA}•\overrightarrow{QB}$是定值，设Q（x₀，y₀），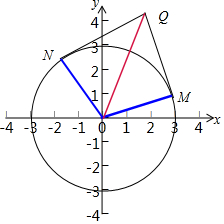
由（Ⅰ）知曲线E：
原点为圆心，$\sqrt{3}$为半径的圆（除A，B点），
∵过E外一点Q作E的两条切线l₁，l₂，且它们的斜率之积为-1，
∴l₁⊥l₂，切点分别是M和N，即QN⊥QM，如图所示：
连接OM、ON、OQ，
由圆的切线的性质得，ON⊥NQ，OM⊥MQ，
∴△ONQ≌△OMQ，则△ONQ是等腰直角三角形，
∵0N=$\sqrt{3}$，∴OQ=3，即${{x}_{0}}^{2}+{{y}_{0}}^{2}=9$，
∴$\overrightarrow{QA}•\overrightarrow{QB}$=（$-\sqrt{3}$-x₀，-y₀）•（$\sqrt{3}-$x₀，0-y₀）
=${{x}_{0}}^{2}-3+{{y}_{0}}^{2}=9-3=6$，
∴$\overrightarrow{QA}•\overrightarrow{QB}$是定值为6．

点评 本题考查轨迹方程的求法，斜率公式、两点之间的距离公式，圆的切线的性质，以及向量的坐标运算和数量积运算，考查数形结合思想，化简、变形能力，分析问题、解决问题的能力．