
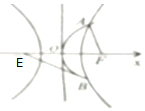 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )| A. | $4+\sqrt{7}$ | B. | $4-\sqrt{3}$ | C. | $4+\sqrt{3}$ | D. | $4-\sqrt{7}$ |
分析 根据双曲线的定义求出|BE|=10a,|BF|=8a,结合抛物线的定义求出交点B的纵坐标,结合直角三角形的边角关系建立方程进行求解即可.
解答 解:根据双曲线和抛物线的对称性得|BF|=|AF|=$\frac{4}{5}$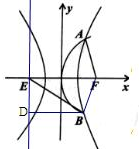 |BE|,
|BE|,
∵|BE|-|BF|=2a,
∴|BE|-$\frac{4}{5}$|BE|=|BE|=2a,
则|BE|=10a,|BF|=8a,
∵抛物线y2=2px(p>0)与双曲线有公共的焦点F,
∴$\frac{p}{2}$=c,且x=-c是抛物线的准线,
则|BD|=|BF|=8a,
设B(x,y),则由抛物线的性质得x+c=8a,即x=8a-c,
代入抛物线方程y2=2px=4cx得y2=4c(8a-c),
则|DE|2=y2=4c(8a-c),
在直角三角形BDE中,
BE2=DE2+BD2,
即100a2=64a2+4c(8a-c),
即36a2-32ac+4c2=0,
即c2-8ac+9a2=0,
解e2-8e+9=0,
得e=$\frac{8±\sqrt{64-36}}{2}$=4±$\sqrt{7}$,
∵0<a<b,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$>$\sqrt{2}$,
∴e=4+$\sqrt{7}$,
故选:A
点评 本题主要考查双曲线离心率的计算,根据抛物线和双曲线的定义建立方程关系,求出a,c的关系是解决本题的关键.综合性较强,有一定的难度.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 《雷雨》只能在周二上演 | B. | 《茶馆》可能在周二或周四上演 | ||
| C. | 周三可能上演《雷雨》或《马蹄声碎》 | D. | 四部话剧都有可能在周二上演 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
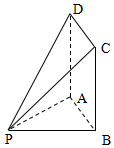 如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{\sqrt{2016}}}$ | B. | $\frac{1}{{\sqrt{2017}}}$ | C. | $\frac{1}{{\sqrt{2018}}}$ | D. | $\frac{1}{{\sqrt{2019}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com