已知f(x)=ax3+bx2+cx+d(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点,若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求实数C的值;
(2)在函数f(x)的图象上是否存在点M(x,y),使f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;不存在说明理由.
【答案】
分析:1由函数极值点定义解得f'(0)=0.
2假设存在 若求出x的值即证明假设否则不存在
解答:解:(1)由已知得f'(x)=3ax
2+2bx+c因为f(x)在[-1,0]和[0,2]上有相反的单调性,
所以x=0是f(x)的一个极值点∴f'(0)=0?∴c=0(4分)
(2)∵c=0,∴f'(x)=3ax
2+2bx
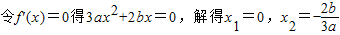
因为f(x)在[0,2]和[4,5]上有相反单调性,

假设存在点M(x
,y
),使得f(x)在点M处的切线斜率为3b,则f'(x
)=3b

∵
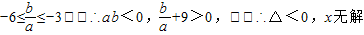
故不存在点M(x
,y
),使得f(x)在点M处的切线斜率为3b(12分)
点评:第一问较简单.第二问进一步考查极值点和 一元二次方程根存在问题

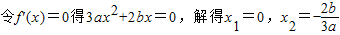




 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案