
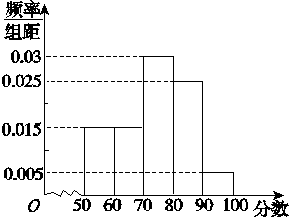
某校从参加高三年级期末考试的学生中抽出60名学生,并统计了他们的历史成绩(成绩均为整数且满分为100分),把其中不低于50分的成绩分成五段[50,60),[60,70),…,[90,100]后,画出部分频率分布直方图(如图),那么这60名学生中历史成绩在[70,80)的学生人数为__________.
科目:高中数学 来源: 题型:
从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的是二等品或三等品”的概率为( )
A.0.7 B.0.65 C.0.35 D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
一个容量为100的样本,其数据的分组与各组的频数如下表
| 组别 | (0,10] | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] | (60,70] |
| 频数 | 12 | 13 | 24 | 15 | 16 | 13 | 7 |
则样本数据落在(10,40]上的频率为( )
A.0.13 B.0.39
C.0. 52 D.0.64
52 D.0.64
查看答案和解析>>
科目:高中数学 来源: 题型:
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
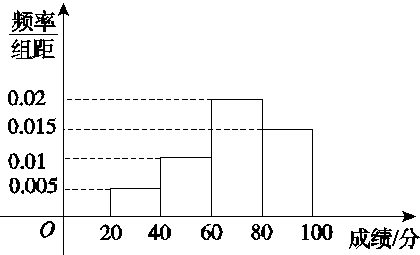
A.45 B.50
C.55 D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得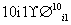 xi=80,
xi=80,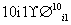 yi=20,
yi=20,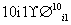 xiyi=184,
xiyi=184,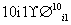 x
x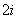 =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,b=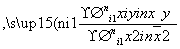 ,a=
,a=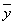 -
- b
b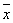 ,
,
其中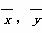 为样本平均值.线性回归方程也可写为
为样本平均值.线性回归方程也可写为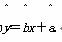
查看答案和解析>>
科目:高中数学 来源: 题型:
小莉与小明一起用A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6)玩游戏,以小莉掷的A立方体朝上的数字为x,小明掷的B立方体朝上的数字为y,来确定点P(x,y),那么他们各掷一次所确定的点P(x,y)落在已知抛物线y=-x2+4x上的概率为( )
A. B.
B.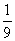
C.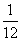 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )
A.(42,56] B.(56,72]
C.(72 ,90] D.(42,90]
,90] D.(42,90]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com