
【题目】已知函数![]()
(1)求函数![]() 的极值点;
的极值点;
(2)当![]() 时,当函数
时,当函数![]() 恰有三个不同的零点,求实数
恰有三个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,无极值点;当
时,无极值点;当![]() 时,有极大值点
时,有极大值点![]() ,无极小值点;(2)
,无极小值点;(2)![]()
【解析】
(1)求出![]() ,对
,对![]() 或
或![]() 是否恒成立做为分类讨论标准,若不恒成立,求出单调区间,进而求出极值,得出结论;
是否恒成立做为分类讨论标准,若不恒成立,求出单调区间,进而求出极值,得出结论;
(2)求出![]() ,要使函数
,要使函数![]() 有三个零点,
有三个零点,![]() 有两个大于零的解,求出
有两个大于零的解,求出![]() 的范围,设
的范围,设![]() 为
为![]() 两个大于零的解,且有
两个大于零的解,且有![]() ,不妨设
,不妨设![]() ,而
,而![]() ,只需求出
,只需求出![]() 在
在![]() 各存在一个零点
各存在一个零点![]() 的范围,即可求出结论.
的范围,即可求出结论.
(1)因为![]() 所以
所以![]() ,
,
所以![]()
![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 无极值点;
无极值点;
当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
由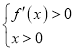 ,解得
,解得![]() ;由
;由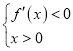 ,解得
,解得![]() .
.
故函数![]() 有极大值点
有极大值点![]() ,无极小值点.
,无极小值点.
综上,当![]() 时,函数
时,函数![]() 无极值点;
无极值点;
当![]() 时,函数
时,函数![]() 有极大值点
有极大值点![]() ,无极小值点.
,无极小值点.
(2)当![]() 时,
时,![]() ,
,
所以![]() ,
,
设![]() ,则
,则![]()
①当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() 不可能有三个不同的零点;
不可能有三个不同的零点;
②当![]() 即
即![]() 时,
时,![]() 有两个零点
有两个零点
![]() ,
,![]() ,
,
所以![]() 又因为
又因为![]() 开口向下,
开口向下,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,又
,又![]() ,所以
,所以![]() ,
,
![]()
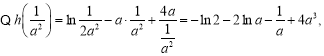
令![]()
则![]() .
.
所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() .
.
由零点存在性定理知,![]() 在区间
在区间![]() 上有唯一的一个零点
上有唯一的一个零点![]() .
.
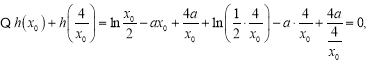
又![]() ,所以
,所以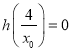 .
.
所以![]() ,所以
,所以![]() 在区间
在区间![]() 上有唯一的一个零点
上有唯一的一个零点![]() ,
,
故当![]() 时,
时,![]() 存在三个不同的零点
存在三个不同的零点![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
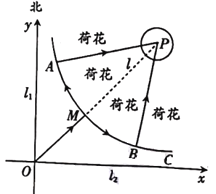
【题目】如图,某市建有贯穿东西和南北的两条垂直公路![]() ,
,![]() ,在它们交叉路口点
,在它们交叉路口点![]() 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台![]() 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线![]() 上,
上,![]() 与环形公路的交点记作
与环形公路的交点记作![]() .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路![]() 先到达环形公路
先到达环形公路![]() 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路![]() ,
,![]() 的环形公路上选
的环形公路上选![]() ,
,![]() 两处(
两处(![]() ,
,![]() 关于直线
关于直线![]() 对称)修建直达观景台
对称)修建直达观景台![]() 的玻璃栈道
的玻璃栈道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的环形公路可用曲线
的环形公路可用曲线![]() 近似表示,曲线
近似表示,曲线![]() 符合函数
符合函数![]() .
.
(1)若![]() 百米,点
百米,点![]() 到
到![]() 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道![]() 的总长度;
的总长度;
(2)若要使得玻璃栈道![]() 的总长度最小为
的总长度最小为![]() 百米,求观景台
百米,求观景台![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点![]() 的轨迹
的轨迹![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与曲线
与曲线![]() 有且仅有一个公共点,与圆
有且仅有一个公共点,与圆![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),求直线
(两点均不在坐标轴上),求直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
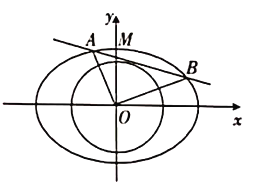
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com