Question

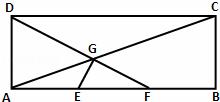
如图，在矩形ABCD中，已知AB=3，AD=1，E、F分别是AB的两个三等分点，AC，DF相交于点G，建立适当的平面直角坐标系：

（1）若动点M到D点距离等于它到C点距离的两倍，求动点M的轨迹围成区域的面积；

（2）证明：E G⊥D F．

Answer 1

考点：

轨迹方程；两条直线垂直的判定．

专题：

直线与圆．

分析：

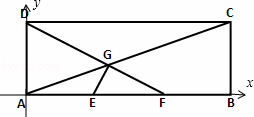
（1）以A为原点，AB所在直线为x轴，建立平面直角坐标系，求出动点M的轨迹方程，即可求出围成区域的面积；

（2）求出直线AC，DF的方程，可得G的坐标，计算k_EG•k_DF=﹣1，即可得到结论．

解答：

（1）解：以A为原点，AB所在直线为x轴，建立平面直角坐标系，则A（0，0），B（3，0），C（3，1），D（0，1），E（1，0），F（2，0）．…（1分）

设M（x，y），由题意知|MD|=2|MC|…（2分）

∴…（3分）

两边平方化简得：即（x﹣4）²+（y﹣1）²=4…（5分）

即动点M的轨迹为圆心（4，1），半径为2的圆，

∴动点M的轨迹围成区域的面积为4π…（6分）

（2）证明：由A（0，0）．C（3，1）知直线AC的方程为：x﹣3y=0，…（7分）

由D（0，1）．F（2，0）知直线DF的方程为：x+2y﹣2=0，…（8分）

由得，故点G点的坐标为．…（10分）

又点E的坐标为（1，0），故k_EG=2，k_DF=﹣   …（12分）

所以k_EG•k_DF=﹣1，即证得：EG⊥DF    …（13分）

点评：

本题考查轨迹方程，考查直线方程的求解，考查学生的计算能力，属于中档题．