
【题目】已知![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ;数列
;数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,问:数列
,问:数列![]() 中是否存在不同两项
中是否存在不同两项![]() ,
,![]() (
(![]() ,i,
,i,![]() ),使
),使![]() 仍是数列
仍是数列![]() 中的项?若存在,请求出i,j;若不存在,请说明理由.
中的项?若存在,请求出i,j;若不存在,请说明理由.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)存在,
,(3)存在,![]() ,
,![]()
【解析】
(1)先根据![]() ,求出
,求出![]() ,再根据
,再根据![]() 可得
可得![]() ,然后两式作差,得到
,然后两式作差,得到![]() ,再求出首项,进而可得数列
,再求出首项,进而可得数列![]() 的通项公式;
的通项公式;
(2)根据![]() ,通过递推,可证数列
,通过递推,可证数列![]() 为等差数列,即可求出通项公式;
为等差数列,即可求出通项公式;
(3)由![]() ,假设数列
,假设数列![]() 中存在不同两项
中存在不同两项![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ),然后根据条件找出满足条件的
),然后根据条件找出满足条件的![]() ,
,![]() 值即可.
值即可.
(1)∵数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]()
∴![]() ,
,![]()
由![]() ,得
,得![]() .
.
∴![]() ,且
,且![]() ,即
,即![]() .
.
∴数列![]() 是首项为
是首项为![]() ,公比为2的等比数列
,公比为2的等比数列
∴![]()
(2)∵![]() ①
①
![]() 时,
时,![]() ②
②
①![]() ②得
②得![]()
∴![]() ,
,![]()
![]() 时,
时,![]() ,∴
,∴![]()
∴![]()
∴![]() 为等差数列
为等差数列
∴![]()
(3)![]() ,假设
,假设![]() 中存在不同的两项
中存在不同的两项![]() ,
,![]() (
(![]() ),使
),使![]() (
(![]() )
)![]()
注意到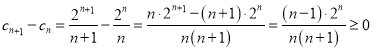 .
.
∴![]() 单调递增
单调递增
由![]() ,则
,则![]() .
.
∴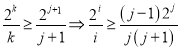
令![]() (
(![]() ),∴
),∴![]()
∴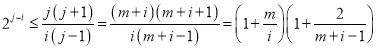
∵![]()
∴![]() ,而
,而![]()
∴![]() ,
,![]()
令![]() ,则
,则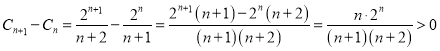
∴![]() 为单调递增,注意到
为单调递增,注意到![]() 时,
时,![]() ,
,![]()
∴m只能为1,2,3
①当![]() 时,
时,![]()
∴![]() ,故i只能为1,2,3
,故i只能为1,2,3
当![]() 时,
时,![]() ,此时
,此时![]()
当![]() 时,
时,![]() ,此时
,此时![]() 无整数解,舍
无整数解,舍
当![]() 时,
时,![]() ,此时
,此时![]() ,无正整数解,舍去
,无正整数解,舍去
②当![]() 时,
时,![]() ,此时
,此时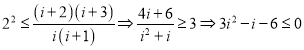
∴![]() ,此时
,此时![]() ,
,![]() 无解
无解
③当![]() 时,
时,![]() ,此时
,此时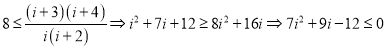 ,无正整数解,舍去.
,无正整数解,舍去.
综上:存在![]() ,
,![]() 满足题意.
满足题意.


科目:高中数学 来源: 题型:
【题目】谈祥柏先生是我国著名的数学科普作家,他写的《数学百草园》、《好玩的数学》、《故事中的数学》等书,题材广泛、妙趣横生,深受广大读者喜爱.下面我们一起来看《好玩的数学》中谈老的一篇文章《五分钟内挑出埃及分数》:文章首先告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).如用两个埃及分数![]() 与
与![]() 的和表示
的和表示![]() 等.从
等.从![]() 这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.曲线
轴的正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com