
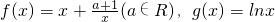 .
.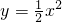 +bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.
+bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.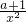
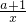 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x0,使得f(x0)<ag(x0)成立,等价于x∈[1,e],Fmin(x)<0
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x0,使得f(x0)<ag(x0)成立,等价于x∈[1,e],Fmin(x)<0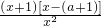
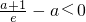
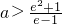
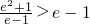 ,∴
,∴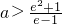
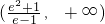 ;
;
 =
= ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b= +b
+b =
= +b
+b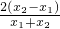 =
=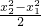 +b(x2-x1)=lnx2-lnx1,
+b(x2-x1)=lnx2-lnx1, =
=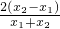 =
=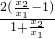
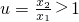 ,在lnu=
,在lnu=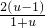 (u>1)①
(u>1)①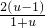 (u>1),则h′(u)=
(u>1),则h′(u)=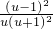
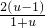
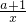 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x0,使得f(x0)<ag(x0)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围;
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x0,使得f(x0)<ag(x0)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围; ,确定C1在P处的切线斜率为k1=
,确定C1在P处的切线斜率为k1= =
= ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b= +b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.
+b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.

科目:高中数学 来源:2011-2012学年安徽省省城名校高三第一次联考数学试卷(理科)(解析版) 题型:解答题
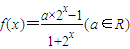 .
.查看答案和解析>>
科目:高中数学 来源:2010年高考数学预测试卷(押题卷1)(解析版) 题型:解答题
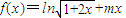 .
.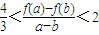 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com