练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．若点M到（0，-3），（0，3）的距离之和等于8，求点M的轨迹方程．

    分析 由题意可知动点的轨迹为以（0，-3），（0，3）为焦点的椭圆，并求出a和c的值，进而可求得b，则椭圆方程可求．

    解答 解：由题意知，动点到两定点（0，-3），（0，3）的距离和为8，且8＞6，
    ∴动点M轨迹是以（0，3），（0，-3）为焦点，长轴长为8的椭圆，
    则a=4，c=3，b2=a2-c2=16-9=7，
    则椭圆的方程为：$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{7}$=1；
    答：点M的轨迹方程为$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{7}$=1．

    点评 本题考查椭圆的定义以及椭圆标准方程的求法，涉及轨迹方程的求法，关键是结合椭圆的定义进行分析．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（2，-1），点O为坐标原点，若向量$\overrightarrow{OA}=3\overrightarrow{a}-\overrightarrow{b}$，$\overrightarrow{BA}=2\overrightarrow{b}-\overrightarrow{a}$，求向量$\overrightarrow{BO}$的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

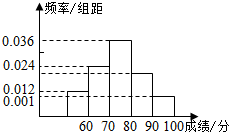    5．对某班的全体学生一次数学测试成绩进行分析，数据的分组情况为：[50，60）[60，70）[70，80）[80，90）[90，100），频率分布直方图如图：
    （Ⅰ）求成绩落在[80，90）之间的频率；
    （Ⅱ）若低于60分的人数是6人，则该班学生人数是多少？
    （Ⅲ）请你估计全班的平均分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．如果函数f（x）在x=x0处的切线的倾斜角是钝角，那么函数f（x）在x=x0附近的变化情况是逐渐下降（填“逐渐上升”或“逐渐下降”）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知log95=m，3n=7，试用含m，n的式子表示log359．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．顶点在原点，坐标轴为对称轴，且焦点在直线2x-3y-6=0上的抛物线方程是y2=12x或x2=-8y．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知$\frac{π}{4}＜x＜\frac{π}{2}$，cos（x-$\frac{π}{4}$）=$\frac{4}{5}$．
    （Ⅰ）求sin（x+$\frac{π}{12}$）的值；
    （Ⅱ）求$\frac{sin2x（1+tanx）}{1-tanx}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．函数y=f（x）的反函数为y=f-1（x），如果函数y=f（x）的图象过点（1，4），那么函数y=f-1（2x）的图象一定过点（2，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知$sin（α-\frac{π}{12}）=\frac{1}{3}$，则$cos（\frac{5π}{12}+α）$=$\frac{1}{3}$．

    查看答案和解析>>

    同步练习册答案