
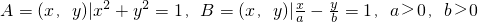 ,当A∩B只有一个元素时,a,b的关系式是________.
,当A∩B只有一个元素时,a,b的关系式是________.
 -
- =1上点坐标构成的集合,又根据两集合的交集只有一个元素,得到直线与圆的位置关系是相切,根据点到直线的距离公式表示出圆心到直线的距离d,让d等于圆的半径,得到关于a与b的一个关系式,化简后得到正确结果.
=1上点坐标构成的集合,又根据两集合的交集只有一个元素,得到直线与圆的位置关系是相切,根据点到直线的距离公式表示出圆心到直线的距离d,让d等于圆的半径,得到关于a与b的一个关系式,化简后得到正确结果. -
- =1,即bx-ay=ab(a>0,b>0)上点坐标构成的集合,
=1,即bx-ay=ab(a>0,b>0)上点坐标构成的集合,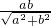 =1,即ab=
=1,即ab= .
.


科目:高中数学 来源:辽宁省大连市、沈阳市2012届高三第二次联合考试数学理科试题 题型:013
在平行四边形ABCD中,∠BAD=60°,AD=2AB,若P是平面ABCD内一点,且满足x![]() +y
+y![]() +
+![]() =
=![]() (x,y∈R),则当点P在以A为圆心,
(x,y∈R),则当点P在以A为圆心,![]() |
|![]() |为半径的圆上时,实数x,y应满足关系式为
|为半径的圆上时,实数x,y应满足关系式为
A.4x2+y2+2xy=1
B.4x2+y2-2xy=1
C.x2+4y2-2xy=1
D.x2+4y2+2xy=1
查看答案和解析>>
科目:高中数学 来源:广东省实验中学2012届高三第一次阶段性测试数学理科试题 题型:044
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy,f(xy)=f(x)f(y)(x,y∈R),且当x≠0时,f(x)≠0.
(1)求证:f(0)=0
(2)证明:f(x)是偶函数.并求f(x)的表达式
(3)若f(x)=alnx有两个不同实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平行四边形ABCD中,∠BAD=60°,AD=2AB,若P是平面ABCD内一点,且满足:x![]() +y
+y![]() +
+![]() =0(x,y∈R).则当点P在以A为圆心,
=0(x,y∈R).则当点P在以A为圆心,![]() |
|![]() |为半径的圆上时,实数x,y应满足关系式为 ( ).
|为半径的圆上时,实数x,y应满足关系式为 ( ).
A.4x2+y2+2xy=1 B.4x2+y2-2xy=1
C.x2+4y2-2xy=1 D.x2+4y2+2xy=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com